
2009年云南省曲靖一中高考冲刺卷理科数学(二)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分.考试时间120分钟.考试结束,将答题卡和答题纸交回. 
第Ⅰ卷(选择题共60分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案.不能答在试卷上.
一、选择题:(每小题5分,共60分)
1.设集合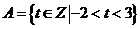 ,
,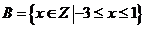 ,
,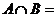 ( )
( )
A.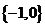 B.
B. C.
C.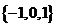 D.
D.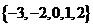

2 设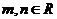 且
且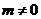 ,若复数
,若复数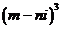 是纯虚数,则( )
是纯虚数,则( )
A.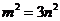 B.
B.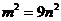 C.
C.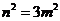 D.
D.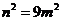

3.函数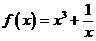 的图象( )
的图象( )
A.关于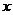 轴对称 B.关于
轴对称 B.关于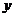 轴对称 C.关于直线
轴对称 C.关于直线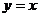 对称 D.关于原点对称
对称 D.关于原点对称
4.若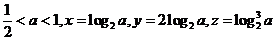 ,则( )
,则( )
A.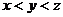 B.
B.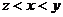 C.
C.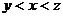 D.
D.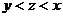

5.已知实数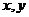 同时满足三个条件:①
同时满足三个条件:① 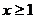 ,②
,②
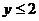 ,③
,③
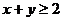 ,则
,则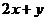 的最
的最
小值等于( )
A.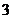 B.
B.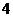 C.
C.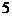 D.
D.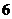

6.从5名男运动员、4名女运动员中任选4名参加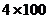 米接力赛跑,则选到的4名运动员中既有男运动员又有女运动员的概率是( )
米接力赛跑,则选到的4名运动员中既有男运动员又有女运动员的概率是( )
A.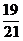 B.
B.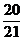 C.
C.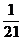 D.
D.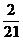

7.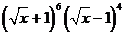 的展开式中
的展开式中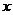 的系数是( )
的系数是( )
A.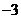 B.
B.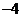 C.
C.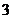 D.
D.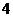

8.已知函数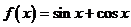 ,
,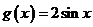 ,动直线
,动直线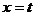 与
与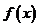 、
、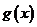 的图象分别交于点
的图象分别交于点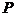 、
、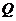 ,则
,则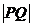 的取值范围是( )
的取值范围是( )
A.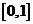 B.
B.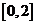 C.
C.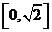 D.
D.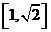

9.设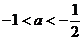 ,则椭圆
,则椭圆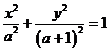 的离心率的取值范围是( )
的离心率的取值范围是( )
A.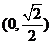 B.
B. C.
C.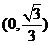 D.
D.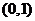

10.正四面体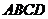 中,
中,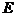 是
是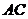 中点,
中点,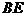 与
与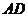 所成角的余弦值等于( )
所成角的余弦值等于( )
A.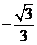 B.
B.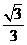 C.
C.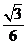 D.
D.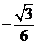

11.某等腰三角形的两腰所在的直线方程是 与
与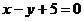 ,点
,点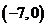 在等腰三角形的底边上,底边所在直线的斜率等于( )
在等腰三角形的底边上,底边所在直线的斜率等于( )
A.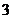 B.
B.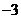 C.
C.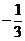 D.
D.

12.正四面体的内切球与外接球的半径的比等于( )
A. B.
B.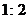 C.
C.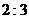 D.
D.

第Ⅱ卷(非选择题共90分)
注意事项:请用黑色中性笔将答案写在答题纸上,在本试卷上作答无效.
二、填空题:(每小题5分,共20分)
13. 已知向量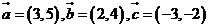 ,
, 与
与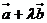 共线,则
共线,则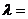 .
.
14. 设曲线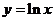 在
在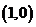 处的切线与直线
处的切线与直线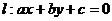 垂直,则直线
垂直,则直线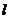 的倾斜角是
弧度.
的倾斜角是
弧度.
15. 曲线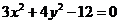 的过焦点且倾斜角是
的过焦点且倾斜角是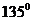 的弦的长度等于 .
的弦的长度等于 .
16. 请写出一个三棱锥是正三棱锥的三个充要条件:
充要条件①
;
充要条件②
;
充要条件③
.
三、解答题:(本大题共6小题,共70分)
17. (本题满分10分)在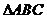 中,
中,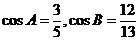 ,
,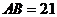 ,求
,求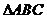 的面积.
的面积.
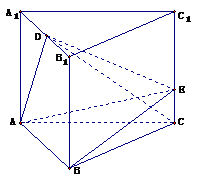 18. (本题满分12分)在正三棱柱
18. (本题满分12分)在正三棱柱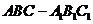 中,
中,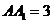 ,
,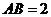 ,
,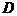 是
是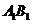 的中点,
的中点,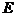 在
在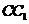 上且
上且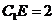 .
.
(Ⅰ)证明: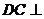 平面
平面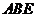 ;
;
(Ⅱ)求二面角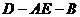 的大小.
的大小.


19. (本题满分12分)关于学平险(即学生平安保险),学生自愿投保,每个投保学生每年缴纳保费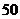 元,如果学生发生意外伤害或符合赔偿的疾病,可获得
元,如果学生发生意外伤害或符合赔偿的疾病,可获得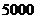 元的赔偿.假定各投保学生是否出险相互独立,并且每个投保学生在一年内出险的概率均是
元的赔偿.假定各投保学生是否出险相互独立,并且每个投保学生在一年内出险的概率均是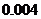 (说明:此处对实际保险问题作了简化处理).假定一年内有
(说明:此处对实际保险问题作了简化处理).假定一年内有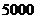 人投保.
人投保.
(Ⅰ)求保险公司在学平险种中,一年内至少支付赔偿金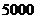 元的概率;
元的概率;
(Ⅱ)设保险公司办理学平险除赔偿金之外的成本为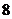 万元,求该公司在学平险种上盈利的期望.
万元,求该公司在学平险种上盈利的期望.


20. (本题满分12分)设数列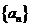 的前
的前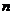 项和为
项和为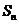 ,满足
,满足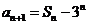 .
.
(Ⅰ)当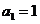 时,用
时,用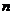 表示
表示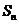 ;
;
(Ⅱ)求首项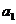 的取值范围,使得
的取值范围,使得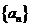 是递减数列.
是递减数列.
21. (本题满分12分)设函数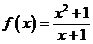 .
.
(Ⅰ)求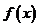 的单调区间及极值;
的单调区间及极值;
(Ⅱ)如果对于任意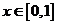 恒有
恒有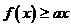 ,求
,求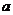 的取值范围.
的取值范围.
22. (本题满分12分)点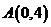 是椭圆
是椭圆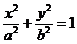 短轴的一个端点,
短轴的一个端点,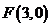 是椭圆的一个焦点,
是椭圆的一个焦点,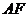 的延长线与椭圆交于点
的延长线与椭圆交于点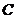 ,直线
,直线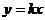 与椭圆相交于点
与椭圆相交于点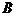 、
、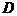 ,与
,与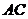 相交于点
相交于点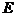 (
(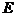 与
与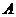 、
、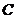 不重合).
不重合).
(Ⅰ)若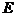 是
是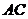 的中点,求
的中点,求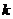 的值;
的值;
(Ⅱ)求四边形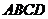 面积的最大值.
面积的最大值.
一、
1.C 2.A 3.D 4.C 5.A 6.B 7.A 8.C 9.D 10.C 
11.D 12.B
1~5略
6. 或
或 .
.
7.解:



 .
.
其展开式中含 的项是:
的项是: ,系数等于
,系数等于 .
.
8.解:根据题意: .
.
9.解: ,椭圆离心率为
,椭圆离心率为 ,
, ,
, .
.
10.解:依腰意作出图形.取 中点
中点 ,连接
,连接 、
、 ,则
,则 ,不妨设四面体棱长为2,则
,不妨设四面体棱长为2,则 是等腰三角形,
是等腰三角形, 必是锐角,
必是锐角, 就是
就是 与
与 所成的角,
所成的角, .
.


11.解:已知两腰所在直线斜率为1, ,设底边所在直线斜率为
,设底边所在直线斜率为 ,已知底角相等,由到角公式得:
,已知底角相等,由到角公式得:


 ,解得
,解得 或
或 .
.
由于等腰三角底边过点( ,0)则只能取
,0)则只能取 .
.
12.解:如图,正四面体 中,
中, 是
是


 中心,连
中心,连 ,此四面体内切球与外接球具有共同球心
,此四面体内切球与外接球具有共同球心 .
. 必在
必在 上,并且
上,并且 等于内切球半径,
等于内切球半径, 等于外接球半径.记
等于外接球半径.记 面积为
面积为 ,则
,则

 ,从而
,从而 .
.
二、
13. .解:
.解: ,
, 与
与 共线
共线 .
.
14. .解:
.解: ,曲线
,曲线 在(1,0)处的切线与直线
在(1,0)处的切线与直线 垂直,则
垂直,则 ,
, 的倾角是
的倾角是 .
.
15.曲线 ①,化作标准形式为
①,化作标准形式为 ,表示椭圆,由于对称性.取焦点
,表示椭圆,由于对称性.取焦点 ,过
,过 且倾角是135°的弦所在直线方程为:
且倾角是135°的弦所在直线方程为: ,即
,即 ②,联立式①与式②.消去y,得:
②,联立式①与式②.消去y,得: ,由弦长公式得:
,由弦长公式得: .
.
16.充要条件①:底面是正三角形,顶点在底面的射影恰是底面的中心.
充要条件②:底面是正三角形.且三条侧棱长相等,
充要条件③:底面是正三角形,且三个侧面与底面所成角相等.
再如:底面是正三角形.且三条侧棱与底面所成角相等;三条侧棱长相等,且三个侧面与底面所成角相等;三个侧面与底面所成角相等,三个侧面两两所成二面角相等.
三、
17.解: ,则
,则 ,
, ,
, .由正弦定理得
.由正弦定理得
 ,
,

 .
.
18.(1)证:已知 是正三棱柱,取
是正三棱柱,取 中点
中点 ,
, 中点
中点 ,连
,连 ,
, ,则
,则 、
、 、
、 两两垂直,以
两两垂直,以 、
、 、
、 为
为 、
、 、
、 轴建立空间直角坐标系,又已知
轴建立空间直角坐标系,又已知 ,
,
则
 .
.
 ,
, ,则
,则 ,又因
,又因 与
与 相交,故
相交,故 面
面 .
.
(2)解:由(1)知, 是面
是面 的一个法向量.
的一个法向量.

 ,设
,设 是面
是面 的一个法向量,则
的一个法向量,则 ①,
①, ②,取
②,取 ,联立式①、②解得
,联立式①、②解得 ,则
,则 .
.
二面角 是锐二面角,记其大小为
是锐二面角,记其大小为 .则
.则
 ,
,
二面角 的大小
的大小 ,亦可用传统方法解(略).
,亦可用传统方法解(略).
19.解:已知各投保学生是否出险相互独立,且每个投保学生在一年内出险的概率都是 ,记投保的5000个学生中出险的人数为
,记投保的5000个学生中出险的人数为 ,则
,则 (5000,0.004)即
(5000,0.004)即 服从二项分布.
服从二项分布.
(1)记“保险公司在学平险险种中一年内支付赔偿金至少5000元”为事件A,则
 ,
,
 .
.
(2)该保险公司学平险除种总收入为 元=25万元,支出成本8万元,支付赔偿金5000
元=25万元,支出成本8万元,支付赔偿金5000 元=0.5
元=0.5 万元,盈利
万元,盈利 万元.
万元.
由 ~
~ 知,
知, ,
,
进而 万元.
万元.
故该保险公司在学平险险种上盈利的期望是7万元.
20.解(1):由 得
得 ,即
,即 ,
,
 ,而
,而

由表可知, 在
在 及
及 上分别是增函数,在
上分别是增函数,在 及
及 上分别是减函数.
上分别是减函数.
 .
.
(2) 时,
时, 等价于
等价于 ,记
,记 ,
,
则 ,因
,因 ,
,
则 在
在 上是减函数,
上是减函数, ,故
,故 .
.
当 时,
时, 就是
就是 ,显然成立,综上可得
,显然成立,综上可得 的取值范围是:
的取值范围是:
22.解:(1)由条件可知椭圆的方程是:

 ①,直线
①,直线 的方程是
的方程是 ②,
②,
联立式①、②消去 并整理得
并整理得 ,由此出发时,
,由此出发时, 是等比数列,
是等比数列,
 .
.
(2)由(1)可知, .当
.当 时,
时,

 ,
,
 是递减数列
是递减数列
对 恒成立
恒成立 .
.
 ,
, 时,
时, 是递减数列.
是递减数列.
21.解(1): ,由
,由 解得函数定义域呈
解得函数定义域呈 .
.
 ,由
,由 解得
解得 ,列表如下:
,列表如下:









0


0


ㄊ
极大
ㄋ
ㄋ
极小
ㄊ
解得 ,进而求得
,进而求得 中点
中点 .
.
己知 在直线
在直线 上,则
上,则 .
.
(2) .
.
设 ,则
,则 ,点
,点 到直线
到直线 的距离
的距离
 .
.
 ,由于直线
,由于直线 与线段
与线段 相交于
相交于 ,则
,则 ,则
,则 .
.
记 ,则
,则 .
.
其次, ,同理求得
,同理求得 到
到 的中离:
的中离: ,
,
设 ,即
,即 ,由
,由 得
得 .
.
 ,
,
即 且
且 时,
时, .
.
又 ,当
,当 即
即 时,
时, .注意到
.注意到 ,由对称性,
,由对称性, 时仍有
时仍有
故 ,进而
,进而 .
.
故四边形 的面积:
的面积:

 ,
,
当 时,
时, .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com