
 亳州一中2008~2009学年度第一学期期中学业水平检测
亳州一中2008~2009学年度第一学期期中学业水平检测
高二 理科数学
一、 选择题:(每小题5分,共60分)
1. 不等式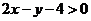 表示的平面区域在直线
表示的平面区域在直线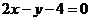 的( )
的( )
 左上方
左上方  右上方
右上方  左下方
左下方 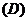 右下方
右下方
2. 样本a1,a2,a3,…,a10的平均数为 ,样本b1,b2,b3,…,b10的平均数为
,样本b1,b2,b3,…,b10的平均数为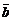 ,那么样本a1,b1,a2,b2,…,a10,b10的平均数为( )
,那么样本a1,b1,a2,b2,…,a10,b10的平均数为( )
A. +
+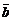 B.
B.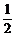 (
( +
+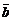 )
)
C.2( +
+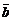 )
D.
)
D.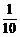 (
( +
+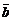 )
)
3.设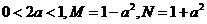 ,
,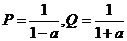 那么( )
那么( )
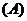
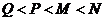
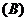
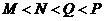

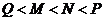
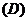
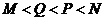
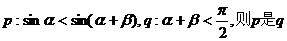 4. 已知
4. 已知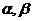 均为锐角,若的( )
均为锐角,若的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
5. 甲、乙两人下一盘棋,甲获胜的概率是40%,甲不输的概率为90%,则甲、乙二人下成和棋的概率为( )
A.60% B.30% C.10% D.50%
6. x为实数,且|x-3|-|x-1|>m能成立,则m的取值范围是( )
A.m>2 B.m<2 C.m>-2 D.m<-2
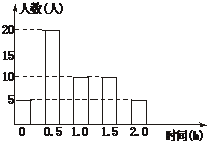
 A.0.6 h B.0.9
h C.1.0 h D.1.5
A.0.6 h B.0.9
h C.1.0 h D.1.5
8. 在如图所示的坐标平面的可行域(阴影部分且包括边界)内,目标函数 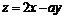 取得最大值的最优解有无数个,则
取得最大值的最优解有无数个,则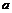 为( )
为( )
A.-2 B.2 C.-6 D.6
9. 在区间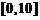 中任意取一个数,则它与
中任意取一个数,则它与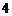 之和大于
之和大于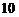 的概率是( )
的概率是( )
A.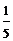 B.
B.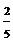 C.
C. 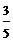 D.
D.
10. 某校高三年级举行一次演讲赛共有10位同学参赛,其中一班有3位,二班有2位,其它班有5位,若采用抽签的方式确定他们的演讲顺序,则一班有3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学没有被排在一起的情况有( )
A.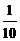 B.
B.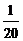 C.
C.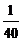 D.
D.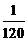
11.
若实数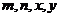 满足
满足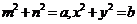
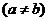 ,则
,则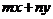 的最大值是( )
的最大值是( )
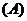
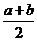
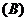
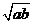

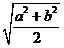
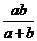
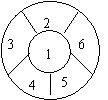 12. 如图:用四种不同的颜色给标有数字的6个区域染色,
12. 如图:用四种不同的颜色给标有数字的6个区域染色,
要求相邻的区域不能染同色,则不同的染色方法有( )
A、192 B、
二、填空题:(每题4分,共4题)
13.
不等式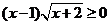 的解集为
的解集为
14. 某校有行政人员、教学人员和教辅人员共200人,其中教学人员与教辅人员的比为10:1,行政人员有24人,现采取分层抽样容量为50的样本那么行政人员应抽取的人数为
15.
设有两个命题:①不等式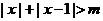 的解集是
的解集是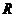 ;②函数
;②函数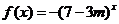 是减函数,如果这两个命题中有且只有一个是真命题,则实数
是减函数,如果这两个命题中有且只有一个是真命题,则实数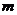 的取值范围是
的取值范围是
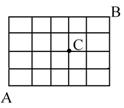 16. 某城市的交通道路如图,从城市的东南角A到城市的西北角B,
16. 某城市的交通道路如图,从城市的东南角A到城市的西北角B,
不经过十字道路维修处C,最近的走法种数有_________________
三、解答题
17. (12分)经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y
(千辆/小时)与汽车的平均速率(千米/小时)之间的函数关系为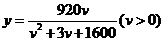 .
.
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?
(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
18. (12分)已知函数 (x
(x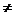 a,a为非零常数).
a,a为非零常数).
(1)解不等式f(x)<x;
(2)设x>a时,f(x)的最小值为6,求a的值。
19. (12分)现有一批产品共有6件,其中4件为正品,2件为次品:
(1)如果从中取出一件,然后放回,再取一件,再放回,求连续3次取出都
为次品的概率;
(2)如果从中取出产品后不放回,求连续取3件至少有一件为次品的概率。
20.(12分)两个CB对讲机持有者, 莉莉和霍伊都为卡尔货运公司工作, 他们的对讲机的接收范围为25公里, 在下午3:0O时莉莉正在基地正东距基地30公里以内的某处向基地行驶,而霍伊在下午3:00时正在基地正北距基地40公里以内的某地向基地行驶,试问在下午3:0O时他们能够通过对讲机交谈的概率有多大?
21.(12分)一化工厂生产某种产品,其生产成本为20元/kg,出厂价为50元/kg,在生产
22. (14分)
(1)若不等式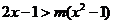 对满足
对满足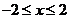 的所有x都成立,求m的取值范围。
的所有x都成立,求m的取值范围。
(2)若不等式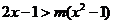 对满足
对满足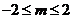 的所有m都成立,求x取值范围。
的所有m都成立,求x取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com