科目：czsx 来源： 题型：
科目：czsx 来源： 题型：
| 1 | 2 |
科目：czsx 来源： 题型：
科目：czsx 来源： 题型：
（2013•东城区二模）如图，在平面直角坐标系中，已知⊙O的半径为1，动直线AB与x轴交于点P（x，0），直线AB与x轴正方向夹角为45°，若直线AB与⊙O有公共点，则x的取值范围是（ ）科目：czsx 来源： 题型：
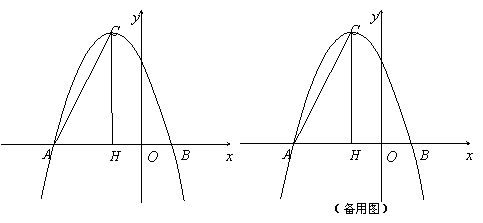
在平面直角坐标系中，抛物线
与
轴的两个交点分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.
（1）根据题意求
，b的值及顶点C的坐标；
（2）在
轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标.
 |
科目：czsx 来源：2013年江苏省海门市中考二模数学试卷（带解析） 题型：单选题
在平面直角坐标系中，平行四边形OABC的顶点为O（0，0）、A（1，2）、B（4，0），则顶点C的坐标是
| A．（-3，2） | B．（5，2） | C．（-4，2） | D．（3，-2） |
科目：czsx 来源：2013年江苏省海门市中考二模数学试卷（解析版） 题型：选择题
在平面直角坐标系中，平行四边形OABC的顶点为O（0，0）、A（1，2）、B（4，0），则顶点C的坐标是
A．（-3，2） B．（5，2） C．（-4，2） D．（3，-2）
科目：czsx 来源：2011年初中毕业升学考试（四川内江卷）数学 题型：解答题
（满分12分）在平面直角坐标系中，抛物线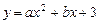
与
轴的两个交点
分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.
（1）直接填写：
= ，b= ，顶点C的坐标为 ；
（2）在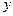
轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标. 
科目：czsx 来源：2011-2012学年湖南省初中毕业学业考试模拟数学试卷9（解析版） 题型：解答题
在平面直角坐标系中，抛物线
与
轴的两个交点分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.
（1）直接填写：
= ，b= ，顶点C的坐标为 ；
（2）在
轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标. 
科目：czsx 来源： 题型：
在平面直角坐标系中，抛物线
与
轴的两个交点分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.
（1）直接填写：
= ，b= ，顶点C的坐标为 ；
（2）在
轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
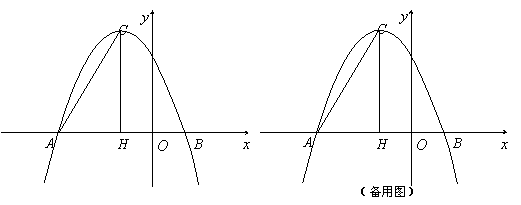（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标.
科目：czsx 来源：2013年北京市东城区中考数学二模试卷（解析版） 题型：选择题
如图，在平面直角坐标系中，已知⊙O的半径为1，动直线AB与x轴交于点P（x，0），直线AB与x轴正方向夹角为45°，若直线AB与⊙O有公共点，则x的取值范围是（ ）
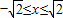
科目：czsx 来源： 题型：
如图，在平面直角坐标系中，直线
与
轴的正半轴、
轴的正半轴分别交于点E和F。从点A（1，0）和
B（3，0）作轴的垂线，分别与直线交于点C和点D。已知
，
求直线的解析式。
 |
科目：czsx 来源： 题型：
如图，在平面直角坐标系
中，点
关于
轴的对称点为
，
与轴交于点
，将△
沿
翻折后，点落在点
处．
（1）求点、的坐标；
（2）求经过
、、三点的抛物线的解析式；
（3）若抛物线的对称轴与交于点
，点
为线段上一点，过点作
轴的平行线，交抛物线于点
．
①当四边形
为等腰梯形时，求出点的坐标；
②当四边形为平行四边形时，直接写出点的坐标.
科目：czsx 来源：2012届湖南省临武县楚江中学初中毕业学业考试模拟数学试卷9（带解析） 题型：解答题
在平面直角坐标系中，抛物线
与
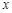轴的两个交点分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.
（1）直接填写：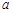
= ，b= ，顶点C的坐标为 ；
（2）在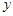
轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标. 
科目：czsx 来源： 题型：
在平面直角坐标系中，点
关于
轴的对称点为
，点关于原点
的对称点为点
．
（1）若点的坐标为
，请你在给出的坐标系中画出
.设
与轴的交点为
， 则
=________;
（2）若点的坐标为
,则的形状为_______.
科目：czsx 来源：2011-2012学年北京市门头沟区九年级上学期期末考试数学试卷（解析版） 题型：解答题
在平面直角坐标系中，抛物线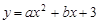
与
轴的两个交点分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.
（1）求抛物线的解析式和顶点坐标；
（2）在
轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标.
与
轴的交点的个数是___________．