
科目:czsx 来源: 题型:

科目:czsx 来源:不详 题型:单选题

| A.t3<t1=t2 | B.t1<t2<t3 | C.t3<t1<t2 | D.t1=t2≤t3 |
科目:czsx 来源: 题型:单选题
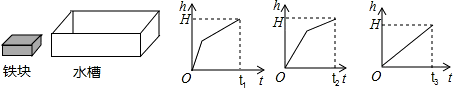
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| k | x |
科目:czsx 来源: 题型:
| k |
| x |
| 1 |
| 2 |
科目:czsx 来源: 题型:
| k |
| x |
| 1 |
| 2 |
A、
| ||
B、
| ||
| C、2009 | ||
| D、2010 |
科目:czsx 来源: 题型:
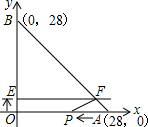 这两个三角形是否相似,请证明你的判断.
这两个三角形是否相似,请证明你的判断. 科目:czsx 来源: 题型:
| k |
| x |
| 1 |
| 2 |
科目:czsx 来源: 题型:
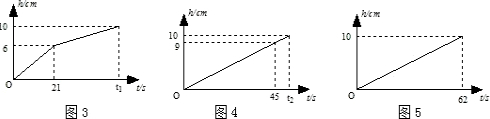
科目:czsx 来源: 题型:阅读理解
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1-2c |
| 2 |
| 1-2c |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1-2c |
| 2 |
| 1-2c |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| m |
| 2 |
| m |
| 2 |
科目:czsx 来源: 题型:
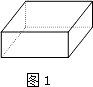
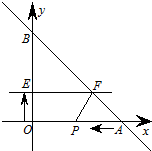 如图,直线y=-x+20与x轴、y轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动.动直线EF从x轴开始以每秒1个长度单位的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于E、F点.连接FP,设动点P与动直线EF同时出发,运动时间为t秒.
如图,直线y=-x+20与x轴、y轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动.动直线EF从x轴开始以每秒1个长度单位的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于E、F点.连接FP,设动点P与动直线EF同时出发,运动时间为t秒.科目:czsx 来源: 题型:
| k | x |
科目:czsx 来源: 题型:
 在平面直角坐标系中,点A1,A2,A3,…,点B1,B2,B3,…,均在x轴上,且OA1=OA2=A2A3=…=An-1An=A1B1=B1B2=B2B3=…=Bn-1Bn=2,分别以OA1,OA2,A2A3,…,An-1An,A1B1,B1B2,B2B3,…,Bn-1Bn为底边的等腰三角形的第三个顶点C1,C2,C3,…,Cn,D1,D2,D3,…,Dn在直线y=x+2上,记△OA1C1的面积为S1,△OA2C2的面积为S2,…,△An-1AnCn的面积为Sn,记△A1B1D1的面积为T1,△B1B2D2的面积为T2,…,△Bn-1BnDn的面积为Tn,那么S1=
在平面直角坐标系中,点A1,A2,A3,…,点B1,B2,B3,…,均在x轴上,且OA1=OA2=A2A3=…=An-1An=A1B1=B1B2=B2B3=…=Bn-1Bn=2,分别以OA1,OA2,A2A3,…,An-1An,A1B1,B1B2,B2B3,…,Bn-1Bn为底边的等腰三角形的第三个顶点C1,C2,C3,…,Cn,D1,D2,D3,…,Dn在直线y=x+2上,记△OA1C1的面积为S1,△OA2C2的面积为S2,…,△An-1AnCn的面积为Sn,记△A1B1D1的面积为T1,△B1B2D2的面积为T2,…,△Bn-1BnDn的面积为Tn,那么S1=科目:czsx 来源: 题型:
| k | x |
科目:czsx 来源: 题型:
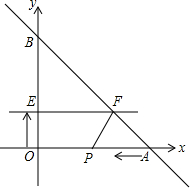 移动(即EF∥x轴),并且分别与y轴、线段AB交于E、F点.(当A运动到点O时,动直线EF随之停止运动) 连接FP,设动点P与动直线EF同时出发,运动时间为t秒.
移动(即EF∥x轴),并且分别与y轴、线段AB交于E、F点.(当A运动到点O时,动直线EF随之停止运动) 连接FP,设动点P与动直线EF同时出发,运动时间为t秒.科目:czsx 来源: 题型:
已知P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(n为正整数)是反比例函数![]() 图象上的点,其中x1=1、x2=2、…、xn=n.记T1=x1·y2、T2=x2·y3、…、T2012=x2012·y2013.若T1=
图象上的点,其中x1=1、x2=2、…、xn=n.记T1=x1·y2、T2=x2·y3、…、T2012=x2012·y2013.若T1=![]() ,则T1·T2·…·T2012=【 】
,则T1·T2·…·T2012=【 】
A.![]() B.
B.![]() C.2012 D.2013
C.2012 D.2013
科目:czsx 来源:2013届浙江省乐清市盐盆一中九年级第三次模拟考试数学试卷(带解析) 题型:解答题
如图,直线y=-x+20与x轴、y轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从x轴开始以每秒1个长度单位的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于E、F点. 连结FP,设动点P与动直线EF同时出发,运动时间为t秒.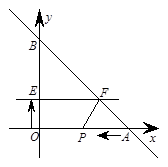
(1) 当t=1秒时,求梯形OPFE的面积;
(2) t为何值时,梯形OPFE的面积最大,最大面积是多少?
(3) 设t的值分别取t1、t2时(t1≠t2),所对应的三角形分别为△AF1P1和△AF2P2.试判断这两个三角形是否相似,请证明你的判断.
科目:czsx 来源: 题型:
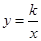 图象上的点,其中x1=1、x2=2、…、xn=n.记T1=x1·y2、T2=x2·y3、…、T2012=x2012·y2013.若T1=
图象上的点,其中x1=1、x2=2、…、xn=n.记T1=x1·y2、T2=x2·y3、…、T2012=x2012·y2013.若T1=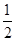 ,则T1·T2·…·T2012=【 】
,则T1·T2·…·T2012=【 】A.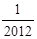 | B.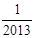 | C.2012 | D.2013 |