科目：czsx 来源： 题型：
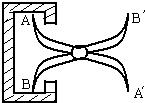12、如图是工厂里常用的可用于测量圆形零件内槽的工具（卡钳），它由两根等长的钢条AB和A′B′在中点处连接而成，只要测出A′B′长就知道AB的长，用到的原理为全等三角形的判定方法科目：czsx 来源： 题型：
科目：czsx 来源： 题型：
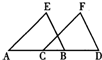13、在学习了全等三角形的判定方法后，刘老师给同学们出了如下的题目：“如图，点C、B在AD上，科目：czsx 来源：2011-2012学年浙江省温州地区初三适应性考试数学卷（解析版） 题型：解答题
（本题6分）在下列四个条件中：①AB=DC；②BE=CE；③∠B=∠C；④∠BAE=∠CDE．请
选出两个作为条件，得出△AED是等腰三角形（写出一个即可），并加以证明．
已知： ▲ ；
求证：△AED是等腰三角形.
证明：
【解析】根据全等三角形的判定和性质求证
科目：czsx 来源： 题型：填空题
如图是工厂里常用的可用于测量圆形零件内槽的工具（卡钳），它由两根等长的钢条AB和A′B′在中点处连接而成，只要测出A′B′长就知道AB的长，用到的原理为全等三角形的判定方法________．科目：czsx 来源：2011-2012学年上海市黄浦区九年级中考二模数学卷（解析版） 题型：解答题
如图，AB是圆O的直径，作半径OA的垂直平分线，交圆O于C、D两点，垂足为H，联结BC、BD.
（1）求证：BC=BD；
（2）已知CD=6，求圆O的半径长.
【解析】本题主要考查全等三角形的判定勾股定理
科目：czsx 来源：《24.3.2 相似三角形的判定》2010年同步练习1（解析版） 题型：填空题
科目：czsx 来源：2011-2012学年北京市朝阳区中考一模数学卷（解析版） 题型：解答题
阅读下面材料：
问题：如图①，在△ABC中， D是BC边上的一点，若∠BAD=∠C=2∠DAC=45°，DC=2．求BD的长．
小明同学的解题思路是：利用轴对称，把△ADC进行翻折，再经过推理、计算使问题
得到解决．
（1）请你回答：图中BD的长为 ；
（2）参考小明的思路，探究并解答问题：如图②，在△ABC中，D是BC边上的一点，若∠BAD=∠C=2∠DAC=30°，DC=2，求BD和AB的长．
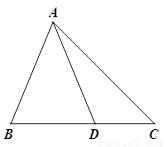
【解析】（1）利用三角形的内角和和角平分线定理进行解答，（2）根据对称的性质、全等三角形的判定和性质以及勾股定理求解
科目：czsx 来源： 题型：
（本题6分）在下列四个条件中：①AB=DC；②BE=CE；③∠B=∠C；④∠BAE=∠CDE．请
选出两个作为条件，得出△AED是等腰三角形（写出一个即可），并加以证明．
已知： ▲ ；
求证：△AED是等腰三角形.
证明：
【解析】根据全等三角形的判定和性质求证
科目：czsx 来源：不详 题型：填空题
科目：czsx 来源： 题型：
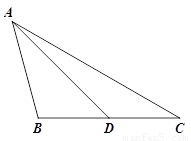
在△ABC中，AB=AC，∠ACB =∠ABC，CG⊥BA交BA的延长线于点G，一等腰三角板按如图27-1所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边
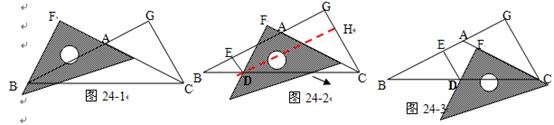
在一条直线上，另一条直角边恰好经过点B。
（1）在图24-1中请你通过观察，测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后说明你的猜想。
（2）当三角尺沿AC方向平移到图24-2所在的位置时，一条直角边仍与AC边在同一直线上，另
一条直角边交BC边于点D，过点D作DE⊥BA于点E，此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE+DF与CG之间满足的数量关系，然后说明你的猜想。
（提示：过点D作DH⊥CG，可得四边形EDHG是长方形，而且∠HDC=∠ABC，ED=GH）
（3）当三角尺在（2）的基础上沿AC方向继续平移到图24-3所示的位置（点F在线段AC上，
且点F与点C不重合）时，试猜想DE、DF与CG之间满足的数量关系？（不用说明理由）
【解析】本题利用等腰直角三角形的性质及全等三角形的判定和性质求解
科目：czsx 来源：不详 题型：单选题
| A．小鹏、小彬和小华 | B．小鹏、小莉和小华 |
| C．小鹏、小彬和小莉 | D．四人回答都正确 |
科目：czsx 来源：学习周报 数学 沪科八年级版 2009－2010学年 第19～26期 总175～182期 沪科版 题型：022
全等三角形的判定方法：对于一般三角形我们可以用“________”、“________”、“________”、“________”这四种方法来判定全等．而对于直角三角形，我们除了可以运用上述四种方法判定全等外，还可以利用一种特殊的判定方法，即“________”．由此，要判定两个三角形全等，至少要有一组________对应相等．
科目：czsx 来源：不详 题型：填空题
科目：czsx 来源： 题型：
【考点】全等三角形的判定与性质；直角梯形；旋转的性质．
【分析】过A作AN⊥BC于N，过E作EM⊥AD，交DA延长线于M，得出四边形ANCD是矩形，推出∠DAN＝90°＝∠ANB＝∠MAN，AD＝NC＝5，AN＝CD，求出BN＝4，求出∠EAM＝∠NAB，证△EAM≌△BNA，求出EM＝BN＝4，根据三角形的面积公式求出即可．
【解答】过A作AN⊥BC于N，过E作EM⊥AD，交DA延长线于M，
∵AD∥BC，∠C＝90°，
∴∠C＝∠ADC＝∠ANC＝90°，
∴四边形ANCD是矩形，
∴∠DAN＝90°＝∠ANB＝∠MAN，AD＝NC＝5，AN＝CD，
∴BN＝9－5＝4，
∵∠M＝∠EAB＝∠MAN＝∠ANB=90°，
∴∠EAM＋∠BAM＝90°，∠MAB＋∠NAB＝90°，
∴∠EAM＝∠NAB，
∵在△EAM和△BNA中，∠M＝∠ANB；∠EAM＝∠BAN；AE＝AB，
∴△EAM≌△BNA（AAS），
∴EM＝BN＝4，
∴△ADE的面积是
×AD×EM＝×5×4＝10．
故选A．
【点评】本题考查了矩形的性质和判定，三角形的面积，全等三角形的性质和判定，主要考查学生运用定理和性质进行推理的能力，题目比较好，难度适中．
科目：czsx 来源： 题型：
如图，AB是圆O的直径，作半径OA的垂直平分线，交圆O于C、D两点，垂足为H，联结BC、BD.
（1）求证：BC=BD；
（2）已知CD=6，求圆O的半径长.
【解析】本题主要考查全等三角形的判定勾股定理
科目：czsx 来源：2011-2012学年北京市朝阳区中考一模数学卷（解析版） 题型：解答题
已知：如图，C是AE的中点，∠B=∠D，BC∥DE．
求证：AB=CD
【解析】利用全等三角形的判定求证
科目：czsx 来源： 题型：阅读理解
阅读下面材料：
问题：如图①，在△ABC中， D是BC边上的一点，若∠BAD=∠C=2∠DAC=45°，DC=2．求BD的长．
小明同学的解题思路是：利用轴对称，把△ADC进行翻折，再经过推理、计算使问题
得到解决．
（1）请你回答：图中BD的长为 ；
（2）参考小明的思路，探究并解答问题：如图②，在△ABC中，D是BC边上的一点，若∠BAD=∠C=2∠DAC=30°，DC=2，求BD和AB的长．
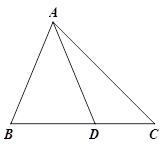
【解析】（1）利用三角形的内角和和角平分线定理进行解答，（2）根据对称的性质、全等三角形的判定和性质以及勾股定理求解
