科目:czsx
来源:
题型:
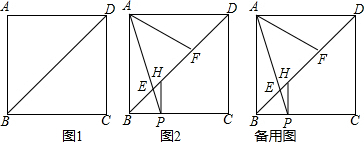
如图1,四边形ABCD是由两个全等的等腰直角三角形斜边重合在一起组成的平面图形.如图2,点P是边BC上一点,PH⊥BC交BD于点H,连接AP交BD于点E,点F为DH中点,连接AF.
(1)求证:四边形ABCD为正方形;
(2)当点P在线段BC上运动时,∠PAF的大小是否会发生变化?若不变,请求出∠PAF的值;若变化,请说明理由;
(3)求证:BE
2+DF
2=EF
2.
查看答案和解析>>
科目:czsx
来源:
题型:
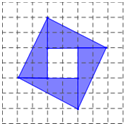
世界数学家大会于2002年在北京举办,大会的会标如图所示,它是由四个全等的直角三角形围成的“弦图”.请你按要求拼图和设计图案.
①每个直角三角形的顶点均在方格纸的格点上;
②每个直角三角形按原来的尺寸画,且互不重叠;
③五个图案互不全等,且不与图1全等.
(1)拼图游戏:应用你所学过的图形变换的知识,将四个直角三角形通过平移、旋转、翻折等方法,拼成以下方格纸中要求的四边形;

(2)设计图案:用四个直角三角形在下列方格纸中按要求设计另外不同的图案.

设计一个既是轴对称图形 设计一个是中心对称图形
又是中心对称图形的图案 但不是轴对称图形的图案.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
世界数学家大会于2002年在北京举办,大会的会标如图所示,它是由四个全等的直角三角形围成的“弦图”.请你按要求拼图和设计图案.
①每个直角三角形的顶点均在方格纸的格点上;
②每个直角三角形按原来的尺寸画,且互不重叠;
③五个图案互不全等,且不与图1全等.
(1)拼图游戏:应用你所学过的图形变换的知识,将四个直角三角形通过平移、旋转、翻折等方法,拼成以下方格纸中要求的四边形;

(2)设计图案:用四个直角三角形在下列方格纸中按要求设计另外不同的图案.

设计一个既是轴对称图形 设计一个是中心对称图形
又是中心对称图形的图案 但不是轴对称图形的图案.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
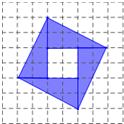 世界数学家大会于2002年在北京举办,大会的会标如图所示,它是由四个全等的直角三角形围成的“弦图”.请你按要求拼图和设计图案.
世界数学家大会于2002年在北京举办,大会的会标如图所示,它是由四个全等的直角三角形围成的“弦图”.请你按要求拼图和设计图案.
①每个直角三角形的顶点均在方格纸的格点上;
②每个直角三角形按原来的尺寸画,且互不重叠;
③五个图案互不全等,且不与图1全等.
(1)拼图游戏:应用你所学过的图形变换的知识,将四个直角三角形通过平移、旋转、翻折等方法,拼成以下方格纸中要求的四边形;
(2)设计图案:用四个直角三角形在下列方格纸中按要求设计另外不同的图案.
设计一个既是轴对称图形 设计一个是中心对称图形
又是中心对称图形的图案 但不是轴对称图形的图案.
查看答案和解析>>
科目:czsx
来源:
题型:
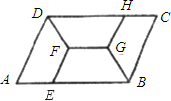
如图,平行四边形ABCD是由4个全等的等腰梯形拼接而成的.
(1)图中的等腰梯形的内角有什么特征?
(2)图中的等腰梯形的边长有什么特征?
(3)请分别用3个这种等腰梯形拼接成一个正三角形,用4个拼接成一个较大的等腰梯形,用6个拼接成一个菱形.(只画出拼图)
查看答案和解析>>
科目:czsx
来源:2010年高级中等学校招生全国统一考试数学卷(浙江台州)
题型:填空题
查看答案和解析>>
科目:czsx
来源:山东省期中题
题型:解答题
如图,平行四边形ABCD是由4个全等的等腰梯形拼接而成的。
(1)图中的等腰梯形的内角有什么特征?
(2)图中的等腰梯形的边长有什么特征?
(3)请分别用3个这种等腰梯形拼接成一个正三角形,用4个拼接成一个较大的等腰梯形,用6个拼接成一个菱形.(只画出拼图)。
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,平行四边形ABCD是由4个全等的等腰梯形拼接而成的.
如图,平行四边形ABCD是由4个全等的等腰梯形拼接而成的.
(1)图中的等腰梯形的内角有什么特征?
(2)图中的等腰梯形的边长有什么特征?
(3)请分别用3个这种等腰梯形拼接成一个正三角形,用4个拼接成一个较大的等腰梯形,用6个拼接成一个菱形.(只画出拼图)
查看答案和解析>>
科目:czsx
来源:2010年高级中等学校招生全国统一考试数学卷(辽宁丹东)
题型:填空题
查看答案和解析>>
科目:czsx
来源:
题型:
如图,圆内接四边形

是由四个全等的等腰梯形组成,
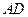
是

的直径,则

为___________度.

查看答案和解析>>
科目:czsx
来源:
题型:
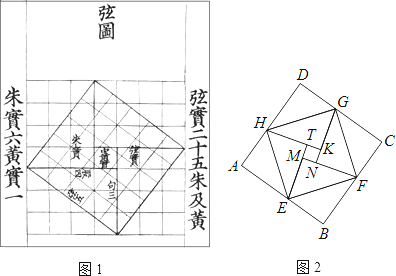
我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S
1,S
2,S
3,若S
1+S
2+S
3=10,则S
2的值是
.
查看答案和解析>>
科目:czsx
来源:
题型:
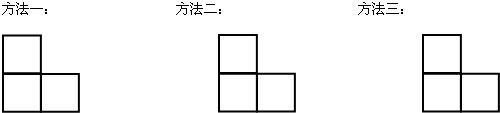
17、如图所示的图形是由3个全等的正方形组成,请你用三种不同的方法分别在原图形上添画一个正方形,使它成为轴对称图形.(画图工具不限,不要求证明,不要求写出画法和结论)
查看答案和解析>>
科目:czsx
来源:2014届浙江建德八年级5月单元检测数学试卷(解析版)
题型:填空题
我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1)。图2由弦图变化得到,它是由八个全等的直角三角形拼接而成。记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=21,则S2的值是 .
查看答案和解析>>
科目:czsx
来源:
题型:
(2011•温州)我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是________.

查看答案和解析>>
科目:czsx
来源:2012-2013学年浙江建德李家镇初级中学八年级5月单元检测数学试卷(带解析)
题型:填空题
我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1)。图2由弦图变化得到,它是由八个全等的直角三角形拼接而成。记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=21,则S2的值是 .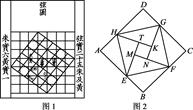
查看答案和解析>>
科目:czsx
来源:2011年初中毕业升学考试(陕西卷)数学解析版
题型:填空题
(2011•温州)我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是________.

查看答案和解析>>
科目:czsx
来源:2011年浙江省温州市中考数学试卷(解析版)
题型:填空题
我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S
1,S
2,S
3,若S
1+S
2+S
3=10,则S
2的值是
.

查看答案和解析>>
科目:czsx
来源:2013年江苏省盐城市盐都区中考数学一模试卷(解析版)
题型:填空题
我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S
1,S
2,S
3,若S
1+S
2+S
3=10,则S
2的值是
.

查看答案和解析>>
科目:czsx
来源:2013年5月中考数学模拟试卷(27)(解析版)
题型:填空题
我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S
1,S
2,S
3,若S
1+S
2+S
3=10,则S
2的值是
.

查看答案和解析>>


 世界数学家大会于2002年在北京举办,大会的会标如图所示,它是由四个全等的直角三角形围成的“弦图”.请你按要求拼图和设计图案.
世界数学家大会于2002年在北京举办,大会的会标如图所示,它是由四个全等的直角三角形围成的“弦图”.请你按要求拼图和设计图案.



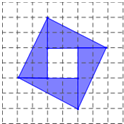
 世界数学家大会于2002年在北京举办,大会的会标如图所示,它是由四个全等的直角三角形围成的“弦图”.请你按要求拼图和设计图案.
世界数学家大会于2002年在北京举办,大会的会标如图所示,它是由四个全等的直角三角形围成的“弦图”.请你按要求拼图和设计图案.

 如图,平行四边形ABCD是由4个全等的等腰梯形拼接而成的.
如图,平行四边形ABCD是由4个全等的等腰梯形拼接而成的. 是由四个全等的等腰梯形组成,
是由四个全等的等腰梯形组成, 是
是 的直径,则
的直径,则 为___________度.
为___________度.

 如图,平行四边形ABCD是由4个全等的等腰梯形拼接而成的.
如图,平行四边形ABCD是由4个全等的等腰梯形拼接而成的. 是由四个全等的等腰梯形组成,
是由四个全等的等腰梯形组成, 是
是 的直径,则
的直径,则 为___________度.
为___________度.








