精英家教网 >
试题搜索列表 >搜索试题．将抛物线向下平移25．将抛物线向下平移2个单位得到的抛物线的解析式为 ，再向上平移3个单位得到的抛物线的解析式为 ，并分别写出这两个函数的顶点坐标 、 个单位得到的将抛物线向下平移2个单位得到的抛物线的解析式为 ，再向上平抛物线的解析式为 ，再向上平移3个单位得到的抛物线的解析式为 ，并分别写出这两个函数的顶点坐标 、
搜索试题．将抛物线向下平移25．将抛物线向下平移2个单位得到的抛物线的解析式为 ，再向上平移3个单位得到的抛物线的解析式为 ，并分别写出这两个函数的顶点坐标 、 个单位得到的将抛物线向下平移2个单位得到的抛物线的解析式为 ，再向上平抛物线的解析式为 ，再向上平移3个单位得到的抛物线的解析式为 ，并分别写出这两个函数的顶点坐标 、 答案解析
科目：czsx
来源：
题型：
4、抛物线y=4x
2-3是将抛物线y=4x
2，向
下
平移
3
个单位得到的．
查看答案和解析>>
科目：czsx
来源：
题型：
2、将抛物线y=3x2向下平移1个单位得到新的抛物线，则新抛物线的解析式是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
2、将一抛物线向下，向右各平移2个单位得到的抛物线是y=-x2，则该抛物线的解析式是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
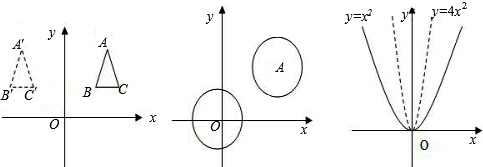
如图1，将△ABC的三个顶点的横坐标同时乘以-1得到三个新的顶点A′，B′，C′，则△ABC与△A′B′C′关于y轴对称（对称变换）；如图2，将⊙O（x
2+y
2=2）向上平移2个单位，在向右平移3个单位得到⊙A （x-3）
2+（y-2）
2=2（平移变换）；如图3，把y=x
2的图象上点的横坐标不变，所有点的纵坐标同时乘以4得到一个新图象，则新图象的解析式为
y=x2，即y=4x
2（伸缩变换）．试回答问题：
（1）y=x
2-x+1的图象关于原点对称图象的解析式为
；
（2）将
y=-的图象向左平移3个单位，再向下平移4个单位，得到的图象的解析式为
；
（3）将y=5x+1的图象所有点的纵坐标不变，横坐标缩短为原来的
，得到的图象的解析式为
；
（4）试探究：抛物线y=3x
2-6x+1是由抛物线y=x
2通过怎样的变换而得到的？
查看答案和解析>>
科目：czsx
来源：
题型：
13、将抛物线y=ax
2+bx+c（a≠0）向下平移3个单位，再向左平移4个单位得到抛物线y=-2x
2-4x+5，则原抛物线的顶点坐标是
（3，10）
．
查看答案和解析>>
科目：czsx
来源：
题型：
若将抛物线y=2x2先向左平移2个单位，再向下平移1个单位得到一个新的抛物线，则新抛物线的顶点坐标是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
将抛物线向左平移4个单位后，再向下平移2个单位得到新抛物线y=（x+2）
2-1，则原抛物线的顶点坐标是
（2，1）
（2，1）
．
查看答案和解析>>
科目：czsx
来源：
题型：
6、将抛物线y=-2x2向右平移3个单位，再向下平移4个单位得到的抛物线的解析式是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
（2012•南安市质检）已知二次函数y=x
2+bx-3（b为常数）的图象经过点（2，-3 ）．
（1）求b的值；
（2）如图，已知点A（1，0）、B（6，0），∠ABC=90°，AB=BC，将△ABC沿x轴向左平移n个单位得到△A′B′C′，若点C′恰好落在第一象限的抛物线上，求n的值；
（3）在（2）的条件下，点M是线段A′C′上一动点（点A′、C′除外），过点M作x轴的垂线交抛物线于点N，当线段MN的长度达到最大时，求以MN为直径的圆与直线A′C′的另一个交点P的坐标．
查看答案和解析>>
科目：czsx
来源：
题型：
（2013•百色）如图，在平面直角坐标系xOy中，将抛物线C
1：y=x
2+3先向右平移1个单位，再向下平移7个单位得到抛物线C
2．C
2的图象与x轴交于A、B两点（点A在点B的左侧）．
（1）求抛物线C
2的解析式；
（2）若抛物线C
2的对称轴与x轴交于点C，与抛物线C
2交于点D，与抛物线C
1交于点E，连结AD、DB、BE、EA，请证明四边形ADBE是菱形，并计算它的面积；
（3）若点F为对称轴DE上任意一点，在抛物线C
2上是否存在这样的点G，使以O、B、F、G四点为顶点的四边形是平行四边形？如果存在，请求出点G的坐标；如果不存在，请说明理由．
查看答案和解析>>
科目：czsx
来源：
题型：
在平面直角坐标系xOy中，抛物线y=mx
2+2
mx+n经过P（
，5），A（0，2）两点．
（1）求此抛物线的解析式；
（2）设抛物线的顶点为B，将直线AB沿y轴向下平移两个单位得到直线l，直线l与抛物线的对称轴交于C点，求直线l的解析式；
（3）在（2）的条件下，求到直线OB，OC，BC距离相等的点的坐标．
查看答案和解析>>
科目：czsx
来源：
题型：
如图，抛物线C
1：y=ax
2+bx+1的顶点坐标为D（1，0），
（1）求抛物线C
1的解析式；
（2）如图1，将抛物线C
1向右平移1个单位，向下平移1个单位得到抛物线C
2，直线y=x+c，经过点D交y轴于点A，交抛物线C
2于点B，抛物线C
2的顶点为P，求△DBP的面积
（3）如图2，连接AP，过点B作BC⊥AP于C，设点Q为抛物线上点P至点B之间的一动点，连接PQ并延长交BC于点E，连接BQ并延长交AC于点F，试证明：FC（AC+EC）为定值．
查看答案和解析>>
科目：czsx
来源：
题型：
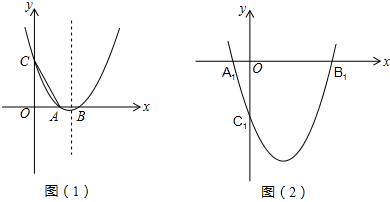
（2011•成华区二模）如图（1），抛物线C：y=x
2+bx+c与x轴正半轴交于A（x
1，0），B（x
2，0）两点，与y轴交于点C（0，2），已知x
1-2x
2=-3．
（1）求抛物线C的解析式；
（2）连接AC．若点P在抛物线C的对称轴上，求使△APC为等腰三角形的点P的坐标；
（3）将图（1）中的抛物线C向下平移6个单位得到图（2）所示的抛物线F．若点M是抛物线F上B
1、C
1间的一个动点（不与B
1、C
1重合），试问是否存在点M使得四边形A
1B
1MC
1的面积最大？若存在，求出点M的坐标和最大面积；若不存在，请说明理由．
查看答案和解析>>
科目：czsx
来源：
题型：阅读理解
（2013•凉山州）先阅读以下材料，然后解答问题：
材料：将二次函数y=-x
2+2x+3的图象向左平移1个单位，再向下平移2个单位，求平移后的抛物线的解析式（平移后抛物线的形状不变）．
解：在抛物线y=-x
2+2x+3图象上任取两点A（0，3）、B（1，4），由题意知：点A向左平移1个单位得到A′（-1，3），再向下平移2个单位得到A″（-1，1）；点B向左平移1个单位得到B′（0，4），再向下平移2个单位得到B″（0，2）．
设平移后的抛物线的解析式为y=-x
2+bx+c．则点A″（-1，1），B″（0，2）在抛物线上．可得：
，解得：
．所以平移后的抛物线的解析式为：y=-x
2+2．
根据以上信息解答下列问题：
将直线y=2x-3向右平移3个单位，再向上平移1个单位，求平移后的直线的解析式．
查看答案和解析>>
科目：czsx
来源：
题型：
12、将抛物线y=-2x
2+1向右平移3个单位，再向下平移两个单位得到抛物线
y=-2（x-3）2-1
．
查看答案和解析>>
科目：czsx
来源：
题型：
把抛物线
y=-x2向左平移2个单位得到抛物线
；若将它向下平移2个单位，得到抛物线
．
查看答案和解析>>
科目：czsx
来源：凉山州
题型：解答题
先阅读以下材料，然后解答问题：
材料：将二次函数y=-x
2+2x+3的图象向左平移1个单位，再向下平移2个单位，求平移后的抛物线的解析式（平移后抛物线的形状不变）．
在抛物线y=-x
2+2x+3图象上任取两点A（0，3）、B（1，4），由题意知：点A向左平移1个单位得到A′（-1，3），再向下平移2个单位得到A″（-1，1）；点B向左平移1个单位得到B′（0，4），再向下平移2个单位得到B″（0，2）．
设平移后的抛物线的解析式为y=-x
2+bx+c．则点A″（-1，1），B″（0，2）在抛物线上．可得：
，解得：
．所以平移后的抛物线的解析式为：y=-x
2+2．
根据以上信息解答下列问题：
将直线y=2x-3向右平移3个单位，再向上平移1个单位，求平移后的直线的解析式．
查看答案和解析>>
科目：czsx
来源：2012年江苏省南京市中考数学模拟试卷（五）（解析版）
题型：解答题
在平面直角坐标系xOy中，抛物线y=mx
2+2
mx+n经过P（
，5），A（0，2）两点．
（1）求此抛物线的解析式；
（2）设抛物线的顶点为B，将直线AB沿y轴向下平移两个单位得到直线l，直线l与抛物线的对称轴交于C点，求直线l的解析式；
（3）在（2）的条件下，求到直线OB，OC，BC距离相等的点的坐标．
查看答案和解析>>
科目：czsx
来源：2009-2010学年北京市清华附中九年级（上）统练数学试卷（12）（解析版）
题型：填空题
将抛物线y=ax2+bx+c（a≠0）向下平移3个单位，再向左平移4个单位得到抛物线y=-2x2-4x+5，则原抛物线的顶点坐标是 ．
查看答案和解析>>
科目：czsx
来源：
题型：
如图，抛物线C1：y=ax2+bx+1的顶点坐标为D（1，0），
（1）求抛物线C1的解析式；
（2）如图1，将抛物线C1向右平移1个单位，向下平移1个单位得到抛物线C2，直线y=x+c，经过点D交y轴于点A，交抛物线C2于点B，抛物线C2的顶点为P，求△DBP的面积
（3）如图2，连接AP，过点B作BC⊥AP于C，设点Q为抛物线上点P至点B之间的一动点，连接PQ并延长交BC于点E，连接BQ并延长交AC于点F，试证明：FC·（AC+EC）为定值．
查看答案和解析>>
