科目：czsx 来源： 题型：044
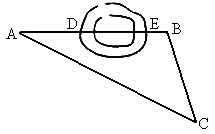
如图所示，为了测量某铁路道口D，E间的距离，在山的一侧选取适当的点C，测得BC=200m，∠B=105°，∠C=45°，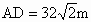
，
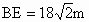，A，D，E，B在同一直线上，求隧道口DE的长．
科目：czsx 来源：中学学习一本通 数学八年级下册 北师大新课标 题型：044
如图所示，要测量河两岸相对两点A，B间的距离，先从B出发与AB成
方向向前走50 m，到C处立一根标杆，然后方向不变继续向前走10 m到D处，在D处转，沿DE方向再走17 m到达E处，恰好A，C，E三点在同一直线上.你能依据题设条件及图形，求出河两岸A，B两点之间的距离吗？
科目：czsx 来源： 题型：013
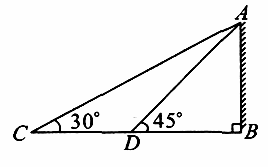
如图所示，为了测量某建筑物的高度，在平地上C处测得建筑物顶端A的仰角为30°，沿CB方向前进12 m到达D处，在D处测得建筑物顶端A的仰角为45°，则建筑物AB的高度等于( )．
A
．
B．
C
．
D．
科目：czsx 来源： 题型：044
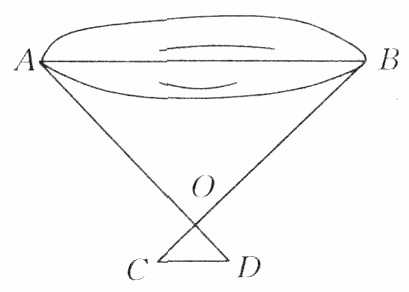
如图所示，为了测量某湖的宽AB，在A，B两处找出两个标志点，然后在岸边找到一点O，沿AO方向确定一点D，作CD平行于AB，使C点与B，O在同一条直线上，这时测得AO=42.5 m，OD=3 m，CD=4.13 m，试求出湖宽AB．(精确到 0.1 m)
科目：czsx 来源： 题型：022
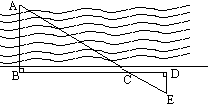
如图所示，为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下的探索：根据科学中光的反射定律，利用一面镜子和一根皮尺，设计如下图所示的测量方案：把一面很小的镜子放在离树底(B)8.4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.4米，观察者目高CD=1.6米，则树(AB)的高度约为______米．(精确到0.1米)
科目：czsx 来源：新课标教材导学 数学八年级第二学期 题型：044
如图，为了测量某铁路上隧道口D、E间的距离，在山的一侧选取适当的点C，测得BC＝200米，∠B＝
，∠C＝
，AD＝18
米，BE＝32
米(A、D、E、B在一条直线上)，计算隧道DE的长度．(精确到0.1米，
＝1.414)
科目：czsx 来源： 题型：
如图所示，为了测量河对岸楼房AB的高度，某中学实践活动小组的同学先在C点测得楼顶A的仰角为30°，沿CB方向前进20m到达D处，在D处测得楼房顶端A的仰角为45°，你能根据以上数据求出楼房的高度吗？（精确到0.1m）科目：czsx 来源：非常讲解·教材全解全析 数学 九年级下 （配北师大课标） 配北师大课标 题型：044
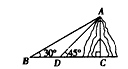
如图所示，为了测量河流某一段的宽度，在河北岸选了一点A，在河南岸选相距200 m的B、C两点，分别测得∠ABC＝60°，∠ACB＝45°，求这段河的宽度．(取
＝1.414，
＝1.732，答案精确到0.1 m)
科目：czsx 来源：三点一测丛书 八年级数学 下 (北京师大版课标本) 北京师大版课标本 题型：044
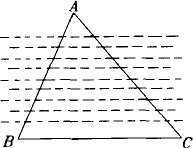
古代一位数学家想出了一种测量某山高的方法：如图所示，为了测量山的高度OB，先竖一根已知长度的木棒
，比较棒子的影长
与山的影长AB，即可近似算出山的高度OB．如果＝1 m，＝2 m，AB＝274 m，求山的高度OB．
科目：czsx 来源： 题型：
离．科目：czsx 来源： 题型：
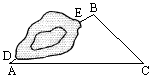
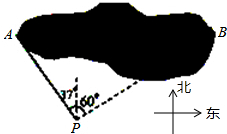
如图所示，为了测量一棵树AB的高度，测量者在D点立一高CD=2m的标杆，现测量者从E处可以看到杆顶C与树顶A在同一条直线上，如果测得BD=20m，FD=4m，EF=1.8m，则树AB的高度为科目：czsx 来源： 题型：
如图所示，为了测量山的高度AC，在水平面B处测得山顶A的仰角为30°，自B沿着BC方向向前走1000m，到达D处，又测得山顶A的仰角为45°，则山高为科目：czsx 来源： 题型：
14、如图所示，为了测量操场上的树高，小明拿来一面小镜子，平放在离树根部12m的地面上，然后他沿着树根和镜子所在直线后退，当他退了4m时，正好在镜中看见树的顶端、若小明的目高为1.6m，则树的高度是科目：czsx 来源： 题型：
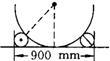27、如图所示，为了测量一个圆形工件的直径，用直径为100mm的两根钢棒嵌在圆形工件的两侧，测得两根棒外侧距离为900mm，那么这个工件的直径是科目：czsx 来源： 题型：
科目：czsx 来源： 题型：
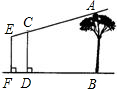如图所示，为了测量一棵树AB的高度，测量者在D点立一高CD=2米的标杆，现测量者从E处可以看到杆顶C与树顶A在同一直线上，如果测得BD=20米，FD=4米，EF=1.8米，则树的高度为科目：czsx 来源： 题型：
果O′B′=1，A′B′=2，AB=274，求金字塔的高度OB． 科目：czsx 来源：101网校同步练习 初三数学 北师大(新课标2001/3年初审) 北师大版 题型：022
如图所示，为了测量河对岸的旗杆AB的高度，在点C处测得旗杆顶端A的仰角为30°，沿CB方向前进5米到达D处，在D处测得旗杆顶端A的仰角为45°，则旗杆AB的高度是________米．
科目：czsx 来源：同步题 题型：解答题
科目：czsx 来源：中华题王 数学 八年级上 (人教版) 人教版 题型：044
如图所示，为了测量河的宽度，在岸边取了A、B，又确定了AB的中点为O，且AB满足AB⊥BC(BC为河宽)，试问应该再怎样做，就可依据角边角公理，不渡河而测量出河宽呢？
