若函数f(x)=a^x(a大于0,a不等于1)上的最大值为4,最小值答案解析
科目:gzsx
来源:
题型:
已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(1)求实数a,b的值;
(2)若不等式f(log2k)>f(2)成立,求实数的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数g(x)=ax
2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(Ⅰ)求实数a,b的值;
(Ⅱ)若不等式f(log
2k)>f(2)成立,求实数k的取值范围;
(Ⅲ)定义在[p,q]上的一个函数m(x),用分法T:p=x
0<x
1<…<x
i<…<x
n=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式
| n |
 |
| i=1 |
|m(xi)-m(xi-1)|≤M恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
| n |
 |
| i=1 |
f(x)=f(x1)+f(x2)+…+f(x
n))
查看答案和解析>>
科目:gzsx
来源:2012-2013学年四川省成都市邛崃市高三(上)12月统考数学试卷(理科)(解析版)
题型:解答题
已知函数g(x)=ax
2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(Ⅰ)求实数a,b的值;
(Ⅱ)若不等式f(log
2k)>f(2)成立,求实数k的取值范围;
(Ⅲ)定义在[p,q]上的一个函数m(x),用分法T:p=x
<x
1<…<x
i<…<x
n=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式
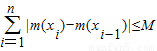
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
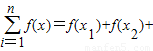
…+f(x
n))
查看答案和解析>>
科目:gzsx
来源:2012-2013学年江苏省泰州市姜堰市高三(上)期中数学试卷(解析版)
题型:解答题
已知函数g(x)=ax
2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(Ⅰ)求实数a,b的值;
(Ⅱ)若不等式f(log
2k)>f(2)成立,求实数k的取值范围;
(Ⅲ)定义在[p,q]上的一个函数m(x),用分法T:p=x
<x
1<…<x
i<…<x
n=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式
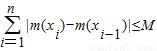
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:

…+f(x
n))
查看答案和解析>>
科目:gzsx
来源:2012-2013学年江苏省泰州市姜堰市高三(上)期中数学试卷(解析版)
题型:解答题
已知函数g(x)=ax
2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(Ⅰ)求实数a,b的值;
(Ⅱ)若不等式f(log
2k)>f(2)成立,求实数k的取值范围;
(Ⅲ)定义在[p,q]上的一个函数m(x),用分法T:p=x
<x
1<…<x
i<…<x
n=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式

恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:

…+f(x
n))
查看答案和解析>>
科目:gzsx
来源:
题型:
若函数f(x)=ax(a>0,a≠1)在[-1,2]上的最大值为4,最小值为m,且函数g(x)=(1-4m)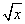 在[0,+∞)上是增函数,则a=________.
在[0,+∞)上是增函数,则a=________.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年山东省烟台市牟平区高三(上)模块检测数学试卷(理科)(解析版)
题型:解答题
已知函数g(x)=ax
2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(Ⅰ)求实数a,b的值;
(Ⅱ)若不等式f(log
2k)>f(2)成立,求实数k的取值范围;
(Ⅲ)定义在[p,q]上的一个函数m(x),用分法T:p=x
<x
1<…<x
i<…<x
n=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式

恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
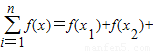
…+f(x
n))
查看答案和解析>>
科目:gzsx
来源:2013-2014学年海南省海口市华兴学校高三(上)第一次月考数学试卷(文科)(解析版)
题型:解答题
已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(1)求实数a,b的值;
(2)若不等式f(log2k)>f(2)成立,求实数的取值范围.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年山东省济宁市曲阜崇德高考补习学校高三(上)期中数学试卷(理科)(解析版)
题型:解答题
已知函数g(x)=ax
2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(Ⅰ)求实数a,b的值;
(Ⅱ)若不等式f(log
2k)>f(2)成立,求实数k的取值范围;
(Ⅲ)定义在[p,q]上的一个函数m(x),用分法T:p=x
<x
1<…<x
i<…<x
n=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式

恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:

…+f(x
n))
查看答案和解析>>
科目:gzsx
来源:2012-2013学年山东省烟台市高三(上)第一学段检测(期中)数学试卷(理科)(解析版)
题型:解答题
已知函数g(x)=ax
2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(Ⅰ)求实数a,b的值;
(Ⅱ)若不等式f(log
2k)>f(2)成立,求实数k的取值范围;
(Ⅲ)定义在[p,q]上的一个函数m(x),用分法T:p=x
<x
1<…<x
i<…<x
n=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式

恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:

…+f(x
n))
查看答案和解析>>
科目:gzsx
来源:2012-2013学年山东省烟台市高三(上)第一学段检测(期中)数学试卷(理科)(解析版)
题型:解答题
已知函数g(x)=ax
2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(Ⅰ)求实数a,b的值;
(Ⅱ)若不等式f(log
2k)>f(2)成立,求实数k的取值范围;
(Ⅲ)定义在[p,q]上的一个函数m(x),用分法T:p=x
<x
1<…<x
i<…<x
n=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式

恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:

…+f(x
n))
查看答案和解析>>
科目:gzsx
来源:
题型:
若函数f(x)=ax(a>0,a≠1)在[-1,2]上的最大值为4,最小值为m,且函数g(x)=(1-4m) 在[0,+∞)上是增函数,则a=________.
在[0,+∞)上是增函数,则a=________.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=

x
3+ax
2+4x的定义域是R,且在区间[-1,1]上是增函数,
(1)求实数a的取值范围;
(2)若函数f(x)的导函数f′(x)在[-1,1]上的最大值为4,试确定函数f(x)的单调区间.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(1)求实数a,b的值;
(2)若不等式f(log2k)>f(2)成立,求实数的取值范围.
查看答案和解析>>
科目:gzsx
来源:数学教研室
题型:044
已知函数f(x)=-3
x2-3
x+4
b2+ (b>
(b>0
)在区间[-b,1
-b]上的最大值为25
.求b的值.
查看答案和解析>>
科目:gzsx
来源:
题型:044
已知函数f(x)=-3x2-3x+4b2+ (b>0)在区间[-b,1-b]上的最大值为25.求b的值.
(b>0)在区间[-b,1-b]上的最大值为25.求b的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
若二次函数f(x)=ax2+2ax+1在区间[-3,2]上的最大值为4,则实数a的值为( )
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax2+2ax+1,
(1)当a=1时,求f(x) 在区间[-3,2]上的值域;
(2)若f(x)在区间[-3,2]上的最大值为4,求实数a的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
若函数f(x)=x2-2x+1在区间a∈[a,a+2]上的最大值为4,则a的值为( )
查看答案和解析>>
科目:gzsx
来源:
题型:
若函数f(x)=x
2-2x+1在区间[a,a+2]上的最大值为4,则a的值为
1或-1
1或-1
.
查看答案和解析>>



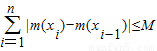 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: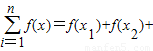 …+f(xn))
…+f(xn))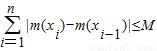 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: …+f(xn))
…+f(xn)) 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: …+f(xn))
…+f(xn))![]() 在[0,+∞)上是增函数,则a=________.
在[0,+∞)上是增函数,则a=________. 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: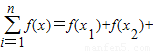 …+f(xn))
…+f(xn)) 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: …+f(xn))
…+f(xn)) 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: …+f(xn))
…+f(xn)) 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: …+f(xn))
…+f(xn))![]() 在[0,+∞)上是增函数,则a=________.
在[0,+∞)上是增函数,则a=________.