
科目:gzsx 来源: 题型:
| 8 |
| 15 |
| 3 |
| 4 |
| 2 |
| 3 |
科目:gzsx 来源:四川省模拟题 题型:解答题
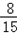 ;
; ,每个男生通过的概率均为
,每个男生通过的概率均为 ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量ξ,求ξ的分布列和数学期望.
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量ξ,求ξ的分布列和数学期望.科目:gzsx 来源:2012年四川省泸州市高考数学二模试卷(理科)(解析版) 题型:解答题
 ;
; ,每个男生通过的概率均为
,每个男生通过的概率均为 ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量ξ,求ξ的分布列和数学期望.
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量ξ,求ξ的分布列和数学期望.科目:gzsx 来源:2011年陕西省咸阳市高考数学三模试卷(理科)(解析版) 题型:解答题
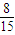 ;
; ,每个男生通过的概率均为
,每个男生通过的概率均为 ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量ξ,求ξ的分布列和数学期望.
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量ξ,求ξ的分布列和数学期望.科目:gzsx 来源:四川省模拟题 题型:解答题
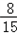 .
. ,每个男生通过的概率均为
,每个男生通过的概率均为 .现对该小组中男生甲.男生乙和女生丙3个人进行测试,求这3人中恰有1人通过测试的概率.
.现对该小组中男生甲.男生乙和女生丙3个人进行测试,求这3人中恰有1人通过测试的概率.科目:gzsx 来源: 题型:
(08年哈三中) 某班艺体特长生中,每人至少具备艺术特长、体育特长两项中的一项,已知具备艺术特长的有2人,具备体育特长的有5人。现从中任选2人,设![]() 为选出的2人中既具备艺术特长又具备体育特长的人数,且
为选出的2人中既具备艺术特长又具备体育特长的人数,且![]() 。
。
(1)求该班艺体特长生的人数;
(2)求![]() 的概率分布,并计算
的概率分布,并计算![]() 的数学期望
的数学期望![]() 。(用数字作答)
。(用数字作答)
科目:gzsx 来源:2014届云南省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
某校高三(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:


(1)求高三(1)班全体女生的人数;
(2)求分数在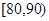 之间的女生人数;并计算频率分布直方图中
之间的女生人数;并计算频率分布直方图中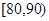 间的矩形的高;
间的矩形的高;
(3)若要从分数在 之间的试卷中任取两份分析女学生失分情况,在抽取的试卷中,求至少有一份分数在
之间的试卷中任取两份分析女学生失分情况,在抽取的试卷中,求至少有一份分数在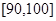 之间的概率.
之间的概率.
科目:gzsx 来源: 题型:
| 8 |
| 15 |
| 3 |
| 4 |
| 2 |
| 3 |
科目:gzsx 来源: 题型:解答题
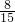 .
. ,每个男生通过的概率均为
,每个男生通过的概率均为 .现对该小组中男生甲.男生乙和女生丙3个人进行测试,求这3人中恰有1人通过测试的概率.
.现对该小组中男生甲.男生乙和女生丙3个人进行测试,求这3人中恰有1人通过测试的概率.科目:gzsx 来源:2012年四川省泸州市高考数学二模试卷(文科)(解析版) 题型:解答题
 .
. ,每个男生通过的概率均为
,每个男生通过的概率均为 .现对该小组中男生甲.男生乙和女生丙3个人进行测试,求这3人中恰有1人通过测试的概率.
.现对该小组中男生甲.男生乙和女生丙3个人进行测试,求这3人中恰有1人通过测试的概率.科目:gzsx 来源: 题型:
某班艺体特长生中,每人至少具备艺术特长、体育特长两项中的一项,已知具备艺术特长的有2人,具有体育特长的有5人.现从中任选2人,若选出的2人中至少有1人既具备艺术特长又具备体育特长的概率为0.7.
(I)求该班艺体特长生的人数;
(II)求选出的2人中恰有1人既具备艺术特长又具备体育特长的概率.(用数字作答)
科目:gzsx 来源: 题型:
| 8 |
| 15 |
| 3 |
| 4 |
| 2 |
| 3 |
科目:gzsx 来源:2011-2012学年江西省高三12周考理科数学 题型:解答题
(本小题满分12分)某企业准备招聘一批大学生到本单位就业,但在签约前要对他们的某项专业技能进行测试.在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为 ;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为 ,每个男生通过的概率均为
,每个男生通过的概率均为 ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量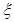 ,求
,求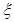 的分布列和数学期望.
的分布列和数学期望.
科目:gzsx 来源: 题型:
(本小题满分13分)某企业准备招聘一批大学生到本单位就业,但在签约前要对他们的某项专业技能进行测试。在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为![]() (I)求该小组中女生的人数; (II)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
(I)求该小组中女生的人数; (II)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为![]() ,每个男生通过的概率均为
,每个男生通过的概率均为![]() ,现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
,现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
科目:gzsx 来源: 题型:
(本小题满分12分)某企业准备招聘一批大学生到本单位就业,但在签约前要对他们的某项专业技能进行测试.在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为![]() ;
;
(Ⅰ)求该小组中女生的人数;
(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为![]() ,每个男生通过的概率均为
,每个男生通过的概率均为![]() ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
科目:gzsx 来源:不详 题型:解答题
| 8 |
| 15 |
| 3 |
| 4 |
| 2 |
| 3 |
科目:gzsx 来源: 题型:
某班艺体特长生中,每人至少具备艺术特长、体育特长两项中的一项,已知具备艺术特长的有2人,具有体育特长的有5人.现从中任选2人,设ξ为选出的2人中既具备艺术特长又具备体育特长的人数,且![]()
(I)求该班艺体特长生的人数;
(II)求ξ的概率分布,并计算ξ的数学期望Eξ.(用数字作答)
科目:gzsx 来源:2012年天津市河西区高考数学一模试卷(理科)(解析版) 题型:解答题
 .
. ,每个男生通过的概率均为
,每个男生通过的概率均为 ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量ξ,求ξ的分布列和数学期望.
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量ξ,求ξ的分布列和数学期望.科目:gzsx 来源: 题型:
| 7 | 10 |