科目：gzsx 来源： 题型：
A.nF=2E B.mV=2E C.V+F=E+2 D.mF=2E
科目：gzsx 来源：2013-2014学年人教版高考数学文科二轮专题复习提分训练5练习卷（解析版） 题型：选择题
设函数f(x)=x2-4x+3,g(x)=3x-2,集合M={x∈R|f(g(x))>0},N={x∈R|g(x)<2},则M∩N为( )
(A)(1,+∞) (B)(0,1)
(C)(-1,1) (D)(-∞,1)
科目：gzsx 来源：南通高考密卷·数学（理） 题型：013
设正多面体的棱数是E，面数是F，顶点数是V，且每个面都是正n边形，以每个顶点为端点的棱有m条，则以下不正确的是
[ ]
科目：gzsx 来源：成功之路·突破重点线·数学（学生用书） 题型：013
设正多面体的棱数是E，面数是F，顶点数是V，且每个面都是正n边形，以每个顶点为端点的棱有m条，则在下列等式中不正确的是
[ ]
科目：gzsx 来源：2011-2012学年山西省朔州市应县四中高一（上）期末模拟考试数学试卷（解析版） 题型：选择题
科目：gzsx 来源：江西省重点中学协作体2012届高三第一次联考数学理科试题 题型：013
设f(x)，g(x)，h(x)是R上的实值函数，如下定义两个函数(f·g)(x)和(f·g)(x)：对任意x∈R，(f·g)(x)＝f(g(x))；(f·g)(x)＝f(x)g(x)，则下列等式恒成立的是
((f·g)·h)(x)＝((f·h)·(g·h))(x)
((f·g)·h)(x)＝((f·h)·(g·h))(x)
((f·g)·h)(x)＝((f·h)·(g·h))(x)
((f·g)·h)(x)＝((f·h)·(g·h))(x)
科目：gzsx 来源：宜都一中2008届高三数学周练(6) 题型：013
设f，g都是由A到B的映射，其中对应法则(从上到下)如下表：
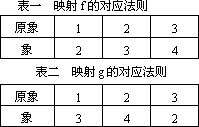
则与f[g(1)]相同的是
A．g[f(1)]
B．g[f(2)]
C．f[g(3)]
D．f[g(1)－1]
科目：gzsx 来源：江西省重点中学协作体2012届高三第一次联考数学文科试题 题型：013
设f(x)，g(x)，h(x)是R上的任意实值函数，如下定义两个函数(f·g)x和(f·g)(x)：对任意x∈R，(f·g)(x)＝f(g(x))；(f·g)(x)＝f(x)g(x)，则下列等式恒成立的是
((f·g)·h)(x)＝((f·h)·(g·h))(x)
((f·g)·h)(x)＝((f·h)·(g·h))(x)
((f·g)·h)(x)＝((f·h)·(g·h))(x)
((f·g)·h)(x)＝((f·h)·(g·h))(x)■(选项一样)
科目：gzsx 来源：0104 期末题 题型：单选题
[ ]
科目：gzsx 来源： 题型：单选题
科目：gzsx 来源：广东省高考真题 题型：单选题
科目：gzsx 来源： 题型：单选题
科目：gzsx 来源： 题型：
.已知函数f(x)=lg(x2-3x+2)的定义域为F，函数g(x)=lg(x-1)+lg(x-2)的定义域为G，那么( )
A.G
F B.G=F C.F
G D.F∩G=
科目：gzsx 来源： 题型：
A.G
F B.G=F C.F
G D.F∩G=
科目：gzsx 来源： 题型：
A.G
F B.G=F C.F
G D.F∩G=
科目：gzsx 来源： 题型：013
函数f(x)＝lg(x2－3x＋2)的定义域为F，函数g(x)＝lg(x－1)＋lg(x－2)的定义域为G，则F与G的关系为（ ）
A. F∩G＝
B. B.F＝G
C.
F
G
D. D.F 
G
科目：gzsx 来源：数学教研室 题型：013
A. F∩G＝
B. B.F＝G
C.
F
G
D. D.F 
G
的定义域为F，g（x）=
的定义域为G，那么集合F、G的关系是( )
G C.G
F D.F∪G=G
的定义域是F,g(x)=
+ 
的定义域是G,则F与G的关系是( )
G B.F
G C.F=G D.F∩G=