(+6）-（+12)-（+7.4）-（ ）=+4答案解析
科目：czsx
来源：
题型：
直角三角形两直角边长度为5，12，则斜边上的高（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
关于x的一元二次方程（a-1）x2+a2-1=0的一个根是x=0，则a等于（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
如图，在直角梯形OABC中，OA∥CB，A、B两点的坐标分别为A（15，0），B（10，12），动点P、Q分别从O、B两点出发，点P以每秒2个单位的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向C运动，当点P停止运动时，点Q也同时停止运动．线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，射线QE交x轴于点F．设动点PQ运
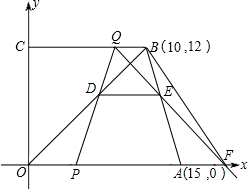
动时间为t（单位：秒）．
（1）当t为何值时，四边形PABQ是等腰梯形，请写出推理过程；
（2）当t=2秒时，求梯形OFBC的面积；
（3）当t为何值时，△PQF是等腰三角形？请写出推理过程．
查看答案和解析>>
科目：czsx
来源：
题型：
某校九年级一班的暑假活动安排中，有一项是小制作评比．作品上交时限为8月1日至30日，班委会把同学们交来的作品按时间顺序每5天组成一组，对每一组的件数进行统计，绘制成如图所示的统计图．已知从左到右各矩形的高度比为2：3：4：6：4：1．第三组的频数是12．请你回答：
（1）本次活动共有
件作品参赛；
（2）上交作品最多的组有作品
件；
（3）经评比，第四组和第六组分别有10件和2件作品获奖，那么你认为这两组中哪个组获奖率较高？为什么？
（4）对参赛的每一件作品进行编号并制作成背面完全一致的卡片，背面朝上的放置，随机抽
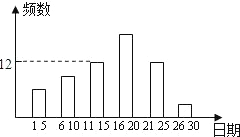
出一张卡片，抽到第四组作品的概率是多少？
查看答案和解析>>
科目：czsx
来源：
题型：
2、正多边形的一个外角的度数为36°，则这个正多边形的边数为（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
古人没有手表，怎样准确掌握时间呢？古人制造线香的本事很大，著名小说家李涵秋笔下，提到过明末清初扬州的一位张老汉，他做的香，形状像一根绳子（材料不均匀），烧完正好需要1小时．无论室内室外、风大风小，都不受影响．现有很多这样的线香，如何通过燃烧这样的线香判断以下时间？（例：
小时怎样判断呢？只要同时点燃一根香的两头，烧完即用
小时）
（1）
小时（即三刻钟） （2）
小时
查看答案和解析>>
科目：czsx
来源：
题型：
计算（-1）
2004+（-
）
-2-（3.14-π）
0．
查看答案和解析>>
科目：czsx
来源：
题型：
百货商场有一种商品的合格率为97%，已知该商品有400件，请问该商场至少还需准备（ ）件商品供消费者更换．
查看答案和解析>>
科目：czsx
来源：
题型：
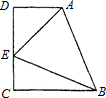
11、如图：直角梯形ABCD中，AD∥CB，∠DCB=90°，AD＜CB，E为CD上一点，∠ABE=45°，AE=10，BC=CD=12，则CE=
4或6
．
查看答案和解析>>
科目：czsx
来源：
题型：
观察下面一列有规律的数：
，
，
，
，
，
，…根据其规律可知：（1）第7个数是
，（2）第n个数应
．
查看答案和解析>>
科目：czsx
来源：
题型：
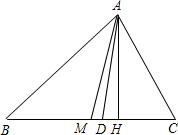
如图，AD、AM、AH分别△ABC的角平分线、中线和高．
（1）因为AD是△ABC的角平分线，所以∠
=∠
=
∠
；
（2）因为AM是△ABC的中线，所以
=
=
；
（3）因为AH是△ABC的高，所以∠
=∠
=90°．
查看答案和解析>>
科目：czsx
来源：
题型：
| A、x≤且x≠0 |
| B、x＞-且x≠0 |
| C、x≠0 |
| D、x＜且x≠0 |
查看答案和解析>>
科目：czsx
来源：
题型：
| A、分式值为零 |
| B、分式无意义 |
| C、若a≠，则分式的值为零 |
| D、若a≠-，则分式的值为零 |
查看答案和解析>>
科目：czsx
来源：
题型：
已知△ABC中，∠C=90°，AB=5，周长为12，则此三角形的内切圆的面积是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
长方形ABCD面积为12，周长为14，则对角线AC的长为
．
查看答案和解析>>
科目：czsx
来源：
题型：
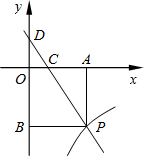
已知：如图，一次函数y=kx+3的图象与反比例函数
y=（x＞0）的图象交于点P．PA⊥x轴于点A，PB⊥y轴于点B．一次函数的图象分别交x轴、y轴于点C、点D，且S
△DBP=27，
=．
（1）求点D的坐标；
（2）求一次函数与反比例函数的解析式；
（3）根据图象写出当x取何值时，一次函数的值小于反比例函数的值？
查看答案和解析>>
科目：czsx
来源：
题型：
7、已知多边形内角和与外角和的和是2160°，则这个多边形的边数是
12
．
查看答案和解析>>
