精英家教网 >
试题搜索列表 >.在直角坐标系中,已知O(0,0),A(2,0),B(0,4),C(0,3),D为x轴上一点.若以D、O、C为顶点的三角形与△AOB相似,这样的D点有( )
.在直角坐标系中,已知O(0,0),A(2,0),B(0,4),C(0,3),D为x轴上一点.若以D、O、C为顶点的三角形与△AOB相似,这样的D点有( )答案解析
科目:czsx
来源:
题型:
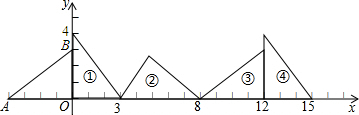
(2013•从化市一模)如图,在直角坐标系中,已知点A(-4,0),B(0,3),对△OAB连续作旋转变换,依次得到三角形(1)、(2)、(3)、(4)、…,那么第(7)个三角形的直角顶点的坐标是
(24,0)
(24,0)
,第(2013)的直角顶点的坐标是
(8052,0)
(8052,0)
.
查看答案和解析>>
科目:czsx
来源:
题型:
在直角坐标系中,已知O(0,0),A(2,0),B(0,4),C(0,3),D为x轴上一点.若以D、O、C为顶点的三角形与△AOB相似,这样的D点有( )
查看答案和解析>>
科目:czsx
来源:
题型:

在直角坐标系中,已知点A(-3,0),点B(0,4),点C是x轴上一点,若△ABC是等腰三角形,试求点C的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在直角坐标系中,已知点A(1,
),O是坐标原点.若连接OA,将线段OA绕点O逆时针旋转90°得到线段OB,则点B的坐标是( )
| A、(,-1) |
| B、(,-1)或(-,1) |
| C、(-,1) |
| D、以上答案都不对 |
查看答案和解析>>
科目:czsx
来源:
题型:
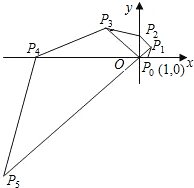
如图,在直角坐标系中,已知点P
0的坐标为(1,0),将线段OP
0按逆时针方向旋转45°,再将其长度伸长为OP
0的2倍,得到线段OP
1;又将线段OP
1按逆时针方向旋转45°,长度伸长为OP
1的2倍,得到线段OP
2;如此下去,得到线段OP
3,OP
4,OP
n(n为正整数),则点P
6的坐标是
;△P
5OP
6的面积是
.
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•泉州质检)如图,在直角坐标系中,已知A(0,3)、O(0,0)、C(6,0)、D(3,3),点P从C点出发,沿着折线C-D-A运动到达点A时停止,过C点作直线GC⊥PC,且与过O、P、C三点的⊙M交于点G,连接OP、PG、OD.设点P运动
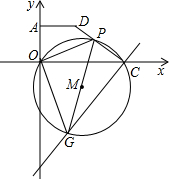
路线的长度为m.
(1)直接写出∠DCO的度数;
(2)当点P在线段CD上运动时,求△OPG的最小面积;
(3)设圆心M的纵坐标为n,试探索:在点P运动的整个过程中,n的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
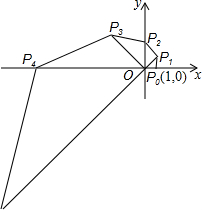
如图,在直角坐标系中,已知点P
0的坐标为(1,0),将线段OP
0按逆时针方向旋转45°,再将其长度伸长为OP
0的2倍,得到线段OP
1;又将线段OP
1按逆时针方向旋转45°,长度伸长为OP
1的2倍,得到线段OP
2;如此下去,得到线段OP
3,OP
4,…,OP
n(n为正整数).我们规定:把点P
n(x
n,y
n)(n=0,1,2,3,…)的横坐标x
n、纵坐标y
n都取绝对值后得到的新坐标(|x
n|,|y
n|)称之为点P
n的“绝对坐标”.则P
n的“绝对坐标”为( )
| A、(2n-1,2n-1)或(2n,0) |
| B、(2n,0)或(0,2n) |
| C、(0,2n)或(2n-1,2n-1) |
| D、(2n-1,2n-1)或(2n,0)或(0,2n) |
查看答案和解析>>
科目:czsx
来源:
题型:
10、在直角坐标系中,已知点A(3,2).作点A关于y轴的对称点为A
1,作点A
1关于原点的对称点为A
2,作点A
2关于x轴的对称点为A
3,作点A
3关于y轴的对称点为A
4,…按此规律,则点A
8的坐标为
(3,-2)
.
查看答案和解析>>
科目:czsx
来源:
题型:
11、在直角坐标系中,已知点P(-3,2),点Q是点P关于x轴的对称点,将点Q向右平移4个单位得到点R,则点R的坐标是
(1,-2)
.
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•新疆)如图1,在直角坐标系中,已知△AOC的两个顶点坐标分别为A(2,0),C(0,2).
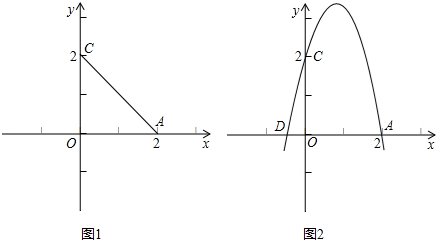
(1)请你以AC的中点为对称中心,画出△AOC的中心对称图形△ABC,此图与原图组成的四边形OABC的形状是
正方形
正方形
,请说明理由;
(2)如图2,已知D(
-,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标;
(3)在问题(2)的图形中,一动点P由抛物线上的点A开始,沿四边形OABC的边从A-B-C向终点C运动,连接OP交AC于N,若P运动所经过的路程为x,试问:当x为何值时,△AON为等腰三角形(只写出判断的条件与对应的结果)?
查看答案和解析>>
科目:czsx
来源:
题型:
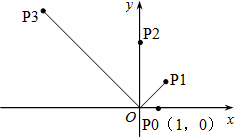
(2013•徐州模拟)如图,在直角坐标系中,已知点P
0的坐标为(1,0),将线段OP
0按逆时针方向旋转45°,再将其长度伸长为OP
0的2倍,得到线段OP
1;又将线段OP
1按逆时针方向旋转45°,长度伸长为OP
1的2倍,得到线段OP
2;如此下去,得到线段OP
3,OP
4,…,OP
n(n为正整数),则点P
2011的坐标为( )
| |
| |
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•塘沽区二模)在直角坐标系中,已知:A(-1,0),B(3,0),C(0,2),以A、B、C、D为顶点的四边形是平行四边形,则D点的坐标为
(2,-2)或(-4,2)或(4,2)
(2,-2)或(-4,2)或(4,2)
.
查看答案和解析>>
科目:czsx
来源:
题型:
在直角坐标系中,已知点A(-3,2),B(2,-4),在x轴上找一点C,使AC+BC最短,则点C的坐标为( )
| A、(0,-) |
| B、(-,0) |
| C、(-4,0) |
| D、(,0) |
查看答案和解析>>
科目:czsx
来源:
题型:
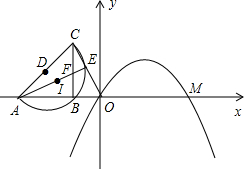
(2007•攀枝花)如图,在直角坐标系中,已知点A、B在x轴上,且B(t,0)(-1<t<0),等腰△ABC的顶点B在以AC为直径的半圆D上,点E是直线OC与半圆D除点C以外的另一个交点,连接AE与BC相交于点F.又已知抛物线y=a(x
2-2x)向左平移2个单位长度后点O恰与点A重合、点M恰与原点O重合,并把平移后所得抛物线记为H.
(1)求证:BF=BO;
(2)如果抛物线H还经过点F,试用含t的式子表示a;
(3)若AE经过△AOC的内心I,试求出此时经过三点A、F、O的抛物线的解析式;
(4)在(3)的条件下,问在抛物线上是否存在点P,使该点关于直线AF的对称点在x轴上?若存在,请求出所有这样的点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•兰州)如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△
1、△
2、△
3、△
4…,则△
2013的直角顶点的坐标为
(8052,0)
(8052,0)
.

查看答案和解析>>
科目:czsx
来源:
题型:阅读理解

阅读材料:
在直角坐标系中,已知平面内A(x
1,y
2)、B(x
1,y
2)两点坐标,则A、B两点之间的距离等于
.
例:说明代数式
+的几何意义,并求它的最小值.
解:
+=
+,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则
可以看成点P与点A(0,1)的距离,
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,所以PA′+PB的最小值为线段A′B的长度.为此,构造直角三角形A′CB,因为A′C=
3
3
,CB=
3
3
,所以A′B=
,即原式的最小值为
.
根据以上阅读材料,解答下列问题:
(1)完成上述填空.
(2)代数式
+
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B
(2,3)
(2,3)
的距离之和.(填写点B的坐标)
(3)求代数式
+的最小值.(画图计算)
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①、②、③、④….
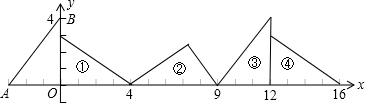
(1)求△OAB的斜边长AB;
(2)三角形⑩有两个顶点落在x轴上,试求点A到最远顶点的距离.
查看答案和解析>>
科目:czsx
来源:
题型:

(2009•南安市质检)如图,在直角坐标系中,已知一次函数y=kx+4的图象与x轴、y轴分别交于点A、B,且与反比例函数
y=(x>0)的图象交于点C(1,n).
(1)求k、n的值;
(2)过点C作CM⊥x轴于点M,求△ACM的内切圆半径(精确到0.01)
查看答案和解析>>
科目:czsx
来源:
题型:

(2012•常州模拟)在直角坐标系中,已知A(0,1),B(10,1),C(9,4).
(1)在网格中画出A、B、C三点的圆和直线y=
x的图象;
(2)已知P是直线y=
x上的点,且△APB是直角三角形,那么符合条件的点P共有
4
4
个;
(3)如果直线y=kx(k>0)上有且只有二个点Q与点A、点B两点构成直角△ABQ.则k=
.
查看答案和解析>>
科目:czsx
来源:
题型:
在直角坐标系中,已知三点A(-5,a)、B(-1,b)和C(2,-4)都在正比例函数y=kx的图象上,则a与b的大小关系是
a>b
a>b
.
查看答案和解析>>


 如图,在直角坐标系中,已知点A(1,
如图,在直角坐标系中,已知点A(1, 如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,OPn(n为正整数),则点P6的坐标是
如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,OPn(n为正整数),则点P6的坐标是 路线的长度为m.
路线的长度为m. 如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数).我们规定:把点Pn(xn,yn)(n=0,1,2,3,…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|)称之为点Pn的“绝对坐标”.则Pn的“绝对坐标”为( )
如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数).我们规定:把点Pn(xn,yn)(n=0,1,2,3,…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|)称之为点Pn的“绝对坐标”.则Pn的“绝对坐标”为( )
 (2013•徐州模拟)如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2011的坐标为( )
(2013•徐州模拟)如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2011的坐标为( ) (2007•攀枝花)如图,在直角坐标系中,已知点A、B在x轴上,且B(t,0)(-1<t<0),等腰△ABC的顶点B在以AC为直径的半圆D上,点E是直线OC与半圆D除点C以外的另一个交点,连接AE与BC相交于点F.又已知抛物线y=a(x2-2x)向左平移2个单位长度后点O恰与点A重合、点M恰与原点O重合,并把平移后所得抛物线记为H.
(2007•攀枝花)如图,在直角坐标系中,已知点A、B在x轴上,且B(t,0)(-1<t<0),等腰△ABC的顶点B在以AC为直径的半圆D上,点E是直线OC与半圆D除点C以外的另一个交点,连接AE与BC相交于点F.又已知抛物线y=a(x2-2x)向左平移2个单位长度后点O恰与点A重合、点M恰与原点O重合,并把平移后所得抛物线记为H.
 阅读材料:
阅读材料: (1)求△OAB的斜边长AB;
(1)求△OAB的斜边长AB; (2009•南安市质检)如图,在直角坐标系中,已知一次函数y=kx+4的图象与x轴、y轴分别交于点A、B,且与反比例函数y=
(2009•南安市质检)如图,在直角坐标系中,已知一次函数y=kx+4的图象与x轴、y轴分别交于点A、B,且与反比例函数y= (2012•常州模拟)在直角坐标系中,已知A(0,1),B(10,1),C(9,4).
(2012•常州模拟)在直角坐标系中,已知A(0,1),B(10,1),C(9,4).