练习册

  • 练习册
  • 试题
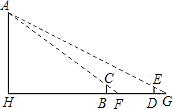
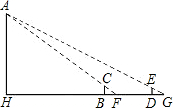    精英家教网 > 试题搜索列表 >三国魏人刘徽，自撰《海岛算经》，专论测高

    三国魏人刘徽，自撰《海岛算经》，专论测高答案解析

    科目：czsx 来源： 题型：

    从下面两个题目中任选一题作答：
    （A题）折竹抵地
    今有竹高一丈，末折抵地，去本三尺．问折者高几何（如图）
    友情提醒：请写出解答这首诗的方法和步骤．
    （B题）海岛算经
    三国魏人刘徽，自撰《海岛算经》，专论测高望远．其中有一题，是数学史上有名的测量问题．今译如下：如图，要测量海岛上一座山峰A的高度AH，立两根高三丈的标杆BC和DE，两竿相距BD=1 000步，D、B、H成一线，从BC退行123步到F，人目着地观察A，A、C、F三点共线；从DE退行127步到G，从G看A，A、E、G三点也共线．试算出山峰的高度AH及HB的距离．（古制1步=6尺，1里=180丈=1 800尺=300步．结果用里和步来表示）
    友情提醒：请写出必要的算法和过程．
    精英家教网精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：

    精英家教网三国魏人刘徽，自撰《海岛算经》，专论测高望远．其中有一题，是数学史上有名的测量问题．今译如下：
    如图，要测量海岛上一座山峰A的高度AH，立两根高三丈的标杆BC和DE，两竿相距BD=1 000步，D、B、H成一线，从BC退行123步到F，人目着地观察A，A、C、F三点共线；从DE退行127步到G，从G看A，A、E、G三点也共线．试算出山峰的高度AH及HB的距离．（古制1步=6尺，1里=180丈=1 800尺=300步．结果用里和步来表示）

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    从下面两个题目中任选一题作答：
    （A题）折竹抵地
    今有竹高一丈，末折抵地，去本三尺．问折者高几何（如图）
    友情提醒：请写出解答这首诗的方法和步骤．
    （B题）海岛算经
    三国魏人刘徽，自撰《海岛算经》，专论测高望远．其中有一题，是数学史上有名的测量问题．今译如下：如图，要测量海岛上一座山峰A的高度AH，立两根高三丈的标杆BC和DE，两竿相距BD=1 000步，D、B、H成一线，从BC退行123步到F，人目着地观察A，A、C、F三点共线；从DE退行127步到G，从G看A，A、E、G三点也共线．试算出山峰的高度AH及HB的距离．（古制1步=6尺，1里=180丈=1 800尺=300步．结果用里和步来表示）
    友情提醒：请写出必要的算法和过程．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    三国魏人刘徽，自撰《海岛算经》，专论测高望远．其中有一题，是数学史上有名的测量问题．今译如下：
    如图，要测量海岛上一座山峰A的高度AH，立两根高三丈的标杆BC和DE，两竿相距BD=1 000步，D、B、H成一线，从BC退行123步到F，人目着地观察A，A、C、F三点共线；从DE退行127步到G，从G看A，A、E、G三点也共线．试算出山峰的高度AH及HB的距离．（古制1步=6尺，1里=180丈=1 800尺=300步．结果用里和步来表示）

    查看答案和解析>>

    科目：czsx 来源：2006年福建省厦门市中考数学试卷（课标B卷）（解析版） 题型：解答题

    （2006•厦门）从下面两个题目中任选一题作答：
    （A题）折竹抵地
    今有竹高一丈，末折抵地，去本三尺．问折者高几何（如图）
    友情提醒：请写出解答这首诗的方法和步骤．
    （B题）海岛算经
    三国魏人刘徽，自撰《海岛算经》，专论测高望远．其中有一题，是数学史上有名的测量问题．今译如下：如图，要测量海岛上一座山峰A的高度AH，立两根高三丈的标杆BC和DE，两竿相距BD=1 000步，D、B、H成一线，从BC退行123步到F，人目着地观察A，A、C、F三点共线；从DE退行127步到G，从G看A，A、E、G三点也共线．试算出山峰的高度AH及HB的距离．（古制1步=6尺，1里=180丈=1 800尺=300步．结果用里和步来表示）
    友情提醒：请写出必要的算法和过程．

    查看答案和解析>>

    科目：czsx 来源：《第24章 图形的相似》2010年综合水平检测题（解析版） 题型：解答题

    三国魏人刘徽，自撰《海岛算经》，专论测高望远．其中有一题，是数学史上有名的测量问题．今译如下：
    如图，要测量海岛上一座山峰A的高度AH，立两根高三丈的标杆BC和DE，两竿相距BD=1 000步，D、B、H成一线，从BC退行123步到F，人目着地观察A，A、C、F三点共线；从DE退行127步到G，从G看A，A、E、G三点也共线．试算出山峰的高度AH及HB的距离．（古制1步=6尺，1里=180丈=1 800尺=300步．结果用里和步来表示）

    查看答案和解析>>

    科目：czsx 来源： 题型：044

    三国魏人刘徽，自撰《海岛算经》，专论测高望远．其中有一题，是数学史上有名的测量问题．今译如下：

    如图，要测量海岛上一座山峰A的高度AH，立两根高三丈的标杆BC和DE，两竿相距BD=1000步，D、B、H成一线，从BC退行123步到F，人目着地观察A，A、C、F三点共线；从DE退行127步到G，从G看A，A、E、G三点也共线．试算出山峰的高度AH及HB的距离．（古制1步=6尺，1里=180丈=1800尺=300步．结果用里和步来表示）

    查看答案和解析>>

    科目：czsx 来源：福建省中考真题 题型：解答题

    国魏人刘徽，自撰《海岛算经》，专论测高望远，其中有一题，是数学史上有名的测量问题，今译如下：如图，要测量海岛上一座山峰A的高度AH，立两根高三丈的标杆BC和DE，两竿相距BD=1000步，D、B、H成一线，从BC退行123步到F，人目着地观察A，A、C、F三点共线；从DE退行127步到G，从G看A，A、E、G三点也共线，试算出山峰的高度AH及HB的距离。（古制1步=6尺，1里=180丈=1 800尺=300步，结果用里和步来表示）

    查看答案和解析>>

    科目：czsx 来源： 题型：044

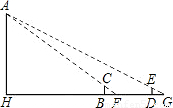
    为了求出海岛上的山峰AB的高度，在D处和F处树立标杆CD和EF，标杆的高都是3丈，D、F两处相隔1000步(1步等于6尺)，并且AB、CD和EF在同一平面内，从标杆DC后退123步的G处，可以看到山峰A和标杆顶端C在一条直线上；从标杆FE后退127步的H处，可看到山峰A和标杆顶端E在一条直线上．求山峰的高度AB及它和标杆CD的水平距离BD各是多少？(提示：连接EC并延长交AB于点K，用AK表示KC及KE．)

    (本题原是我国魏晋时期数学家刘徽所著《海岛算经》中的第一题：今有望海岛，立两表齐高三丈，前后相去千步，令后表与前表参相直．从前表却行一百二十三步，人目着地，取望岛峰，与表末参合．从后表却行一百二十七步，人目着地，取望岛峰，亦与表末参合．问岛高及去表各几何？)

    查看答案和解析>>

    科目：czsx 来源： 题型：

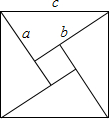    我国古代把直角三角形中较短的直角边称为勾，较长的称为股，斜边称为弦．如图称为“弦图”，最早是由三国时期的数学家赵爽在《周髀算经》中给出的，你能根据“弦图”说明勾股定理的正确性吗？（并写出解答过程）

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    我国古代把直角三角形中较短的直角边称为勾，较长的称为股，斜边称为弦．如图称为“弦图”，最早是由三国时期的数学家赵爽在《周髀算经》中给出的，你能根据“弦图”说明勾股定理的正确性吗？（并写出解答过程）

    查看答案和解析>>

    科目：czsx 来源： 题型：

    13、我国三国时代著名数学家刘徽是第一个用割圆术找到计算圆周率方法的人，他求出π的近似值为3.1416，如果取3.142，是精确到
    千分
    位，有
    4
    个有效数字．

    查看答案和解析>>

    科目：czsx 来源：不详 题型：填空题

    我国三国时代著名数学家刘徽是第一个用割圆术找到计算圆周率方法的人，他求出π的近似值为3.1416，如果取3.142，是精确到______位，有______个有效数字．

    查看答案和解析>>

    科目：czsx 来源：江西省期中题 题型：填空题

    我国三国时代著名数学家刘徽是第一个用割圆术找到计算圆周率方法的人，他求出π的近似值为3.1416，如果取3.142，是精确到（     ）位，有（     ）个有效数字

    查看答案和解析>>

    科目：czsx 来源：浙江省期中题 题型：填空题

    我国三国时代著名数学家刘徽是第一个用割圆术找到计算圆周率方法的人，他求出π的近似值为3.1416，如果取3.142，是精确到（    ）位，有（    ）个有效数字．

    查看答案和解析>>

    科目：czsx 来源： 题型：填空题

    我国三国时代著名数学家刘徽是第一个用割圆术找到计算圆周率方法的人，他求出π的近似值为3.1416，如果取3.142，是精确到________位，有________个有效数字．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    13、我国古代著名数学家刘徽，是世界上第一个利用“割圆术”来计算圆周率的人，他求出π≈3.1416，这个近似数有
    5
    个有效数字．

    查看答案和解析>>

    科目：czsx 来源：竞赛题 题型：单选题

    在中国古代，哪个人首创了一种称为“割圆术”的数学方法，算出π的近似值为3.1416．
    [     ]
    A．祖冲之
    B．刘徽
    C．张衡
    D．杨辉

    查看答案和解析>>

    科目：czsx 来源： 题型：填空题

    我国古代著名数学家刘徽，是世界上第一个利用“割圆术”来计算圆周率的人，他求出π≈3.1416，这个近似数有________个有效数字．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    坐标思想是由下列那位数学家创立的（　　）

    查看答案和解析>>