
科目:czsx 来源: 题型:
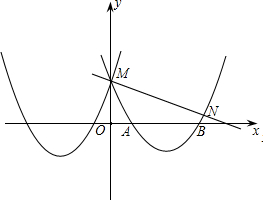 点M,与x轴交于点A和B.
点M,与x轴交于点A和B.科目:czsx 来源: 题型:
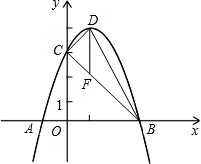 如图已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).设抛物线的顶点为D,求解下列问题:
如图已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).设抛物线的顶点为D,求解下列问题:科目:czsx 来源: 题型:
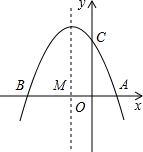 如图已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
如图已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.科目:czsx 来源: 题型:

科目:czsx 来源: 题型:解答题
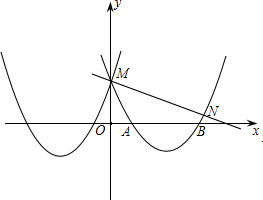 点M,与x轴交于点A和B.
点M,与x轴交于点A和B.科目:czsx 来源: 题型:
 ,其顶点为B(m,3),C是AB中点,
,其顶点为B(m,3),C是AB中点,
 求BD的长;
求BD的长; ,请直接写出此时E点的
,请直接写出此时E点的科目:czsx 来源:2013届江苏省泰州市民兴实验中学九年级上学期期末考试数学试卷(带解析) 题型:单选题
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对
应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;
若y1=y2,记M= y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时
M="0." 下列判断:
①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在;④使得M=1的x值是 或
或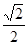 .
.
其中正确的是
| A.①② | B.①④ | C.②③ | D.③④ |
科目:czsx 来源: 题型:
如图, 已知抛物线与x轴相交于A、B,点B的坐标为(10,0),顶点M的坐标为(4,8),点P从点M出发,以每秒1个单位的速度沿线段MA向A点运动;点Q从点A出发,以每秒2个单位的速度沿AB向B点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟。
(1)求抛物线的解析式;
(2)设△APQ的面积为S,求S与t之间的函数关系式,△APQ的面积是否有最大值?若有,请求出其最大值;若没有,请说明理由;
(3)当t为何值时,△APQ为等腰三角形?
科目:czsx 来源:2012年北师大版初中数学九年级下2.8二次函数与一元二次方程练习卷(解析版) 题型:解答题
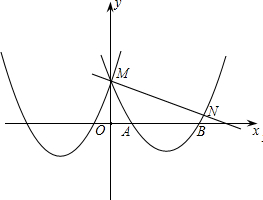
如图,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0),且x1+x2="4,"  .
.
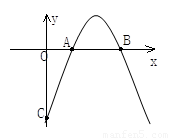
(1)求抛物线的代数表达式;
(2)设抛物线与y轴交于C点,求直线BC的表达式;
(3)求△ABC的面积.
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2011年江苏省泰州市泰兴市洋思中学中考数学二模试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:
如图, 已知抛物线![]() 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
(1)求抛物线的解析式;
(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连结DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P,使△ACP为等腰三角形,若存在,求点P的坐标,若不存在,说明理由.

科目:czsx 来源:2013-2014学年福建省九年级上学期期末考试数学试卷(A)(解析版) 题型:解答题
如图,已知抛物线 与坐标轴交于
与坐标轴交于 三点,点
三点,点 的横坐标为
的横坐标为 ,过点
,过点 的直线
的直线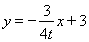 与
与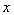 轴交于点
轴交于点 ,点
,点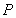 是线段
是线段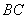 上的一个动点,
上的一个动点, 于点
于点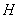 .若
.若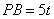 ,且
,且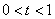 .
.

(1)求 的值
的值
(2)求出点 的坐标(其中
的坐标(其中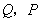 用含
用含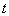 的式子表示):
的式子表示):
(3)依点 的变化,是否存在
的变化,是否存在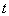 的值,使
的值,使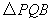 为等腰三角形?
为等腰三角形?
科目:czsx 来源:2012届江苏盐城中学中考模拟考试(二)数学试卷(带解析) 题型:解答题
如图, 已知抛物线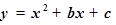 与y轴相交于C,与x轴相交于A、B,点A的坐标为(-1,0),点C的坐标为(0,-3),抛物线的顶点为D.
与y轴相交于C,与x轴相交于A、B,点A的坐标为(-1,0),点C的坐标为(0,-3),抛物线的顶点为D.
【小题1】求抛物线的解析式和顶点D的坐标
【小题2】二次函数的图像上是否存在点P,使得S△PAB=8S△ABD?若存在,求出P点坐标;若不存在,请说明理由;
【小题3】若抛物线的对称轴与x轴交于E点,点F在直线BC上,点M在的二次函数图像上,如果以点F、M、D、E为顶点的四边形是平行四边形,请你求出符合条件的点M的坐标.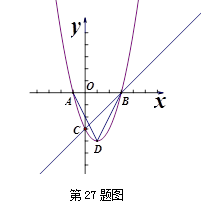
科目:czsx 来源:2011-2012年北京海淀区九年级第一学期期末考试数学卷 题型:解答题
如图, 已知抛物线经过坐标原点O及 ,其顶点为B(m,3),C是AB中点,
,其顶点为B(m,3),C是AB中点,
点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上, 且EO=ED .
【小题1】(1)求此抛物线及直线OC的解析式;
【小题2】(2)当点E运动到抛物线上时,  求BD的长;
求BD的长;
【小题3】(3)连接AD, 当点E运动到何处时,△AED的面积为 ,请直接写出此时E点的
,请直接写出此时E点的
坐标.
科目:czsx 来源:2005年高级中等学校招生全国统一考试数学卷(广东深圳) 题型:解答题
如图, 已知抛物线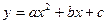 与x轴相交于A、B,点B的坐标为(10,0),顶点M的坐标为(4,8),点P从点M出发,以每秒1个单位的速度沿线段MA向A点运动;点Q从点A出发,以每秒2个单位的速度沿AB向B点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟。
与x轴相交于A、B,点B的坐标为(10,0),顶点M的坐标为(4,8),点P从点M出发,以每秒1个单位的速度沿线段MA向A点运动;点Q从点A出发,以每秒2个单位的速度沿AB向B点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟。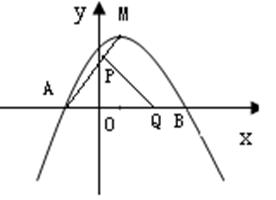
(1)求抛物线的解析式;
(2)设△APQ的面积为S,求S与t之间的函数关系式,△APQ的面积是否有最大值?若有,请求出其最大值;若没有,请说明理由;
(3)当t为何值时,△APQ为等腰三角形?
科目:czsx 来源:2009-2010学年河南省周口市九年级(上)期末数学试卷(解析版) 题型:解答题

科目:czsx 来源:2013-2014学年江苏省无锡市惠山北片九年级上学期期末考试数学试卷(解析版) 题型:选择题
.如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0. 下列判断:
①当x>0时,y1>y2;
②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在;
④使得M=1的x值是 或
或 .其中正确的是( )
.其中正确的是( )

A.①② B.①④ C.②③ D.③④
科目:czsx 来源:2009-2010学年河南省周口市扶沟县九年级(上)期末数学试卷(解析版) 题型:解答题

科目:czsx 来源:2012届山西省临汾市平阳中学九年级下学期第一次月考试卷(带解析) 题型:解答题
如图, 已知抛物线 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
(1)求抛物线的解析式;
(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连结DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P,使△ACP为以AC为腰的等腰三角形,若存在,求点P的坐标,若不存在,说明理由.