科目:gzsx
来源:2011-2012学年浙江省金华十校高三上学期期末考试文科数学(解析版)
题型:填空题
查看答案和解析>>
科目:gzsx
来源:
题型:
已知P(1,2)为圆x
2+y
2=9内一定点,过P作两条互相垂直的任意弦交圆于点B、C,则BC中点M的轨迹方程为
.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知二次函数f(x)=x2-2x+t与两坐标轴分别交于不同的三点A、B、C.
(1)求实数t的取值范围;
(2)当t=-3时,求经过A、B、C三点的圆F的方程;
(3)过原点作两条相互垂直的直线分别交圆F于M、N、P、Q四点,求四边形MPNQ的面积的最大值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知P(1,2)为圆x
2+y
2=9内一定点,过P作两条互相垂直的任意弦交圆于点B、C,则BC中点M的轨迹方程为________.
查看答案和解析>>
科目:gzsx
来源:2014届安徽省六校教育研究会高三素质测试文科数学试卷(解析版)
题型:解答题
已知二次函数 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C.
(1)求实数t的取值范围;
(2)当 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程;
(3)过原点作两条相互垂直的直线分别交圆F于M、N、P、Q四点,求四边形 的面积的最大值。
的面积的最大值。
查看答案和解析>>
科目:gzsx
来源:
题型:
已知P(1,2)为圆x
2+y
2=9内一定点,过P作两条互相垂直的任意弦交圆于点B、C,则BC中点M的轨迹方程为________.
查看答案和解析>>
科目:gzsx
来源:2006年高考第一轮复习数学:7.5 圆的方程(解析版)
题型:解答题
已知P(1,2)为圆x2+y2=9内一定点,过P作两条互相垂直的任意弦交圆于点B、C,则BC中点M的轨迹方程为 .
查看答案和解析>>
科目:gzsx
来源:设计必修二数学北师版 北师版
题型:044
已知P(1,2)为圆x2+y2=9内一定点,过P作两条互相垂直的任意弦交圆于B、C两点,求B、C中点M的轨迹方程.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知P(1,2)为圆x2+y2=9内一定点,过P作两条互相垂直的任意弦交圆于点B、C,则BC中点M的轨迹方程为____________
查看答案和解析>>
科目:gzsx
来源:
题型:填空题
已知P(1,2)为圆x2+y2=9内一定点,过P作两条互相垂直的任意弦交圆于点B、C,则BC中点M的轨迹方程为________.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知抛物线y2=4x的焦点为F,过F作两条相互垂直的弦AB,CD,设弦AB,CD的中点分别为M,N.求证:直线MN恒过定点.
查看答案和解析>>
科目:gzsx
来源:2012年苏教版高中数学选修2-1 2.6曲线的方程练习卷(解析版)
题型:选择题
查看答案和解析>>
科目:gzsx
来源:2013年高考数学复习卷D(八)(解析版)
题型:解答题
已知抛物线y2=4x的焦点为F,过F作两条相互垂直的弦AB,CD,设弦AB,CD的中点分别为M,N.求证:直线MN恒过定点.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知F是双曲线
-=1的一个焦点,过F作一条与坐标轴不垂直,且与渐进线也不平行的直线l,交双曲线于A,B两点,线段AB的中垂线l′交x轴于M点.
(1)设F为右焦点,l的斜率为1,求l′的方程;
(2)试判断
是否为定值,说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知椭圆C
1:
+=1(a>b>0)的离心率为
,一个焦点坐标为
F(-,0).
(1)求椭圆C
1的方程;
(2)点N是椭圆的左顶点,点P是椭圆C
1上不同于点N的任意一点,连接
NP并延长交椭圆右准线与点T,求
的取值范围;
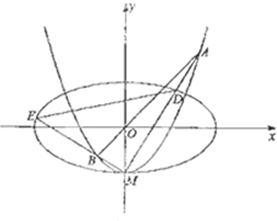
(3)设曲线
C2:y=x2-1与y轴的交点为M,过M作两条互相垂直的直线与曲线C
2、椭圆C
1相交于点A、D和B、E,(如图),记△MAB、
△MDE的面积分别是S
1,S
2,当
=时,求直线AB的方程.
查看答案和解析>>
科目:gzsx
来源:
题型:
下图所示树形图形中.第一层是一与水平线垂直的线段,长度为1;第二层在第一层线段的前端作两条与该段均成135°的线段,长度为其一半;第三层按第二层的方法在每一线段的前端生成两条线段;重复前面的作法作图至第n层.设树形图的第n层的最高点到水平线的距离为第n层树形图的高度.
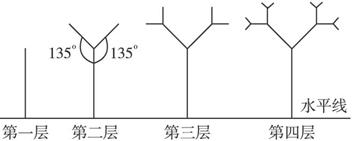
(1)求第三层及第四层树形图的高度H3,H4;
(2)求第n层树形图的高度Hn;
(3)若树形图的高度大于2,则称树形图为“高大”,否则称为“矮小”.显然,当n=1,2时是“矮小”的,是否存在m∈Z,使得当n>m时,该树形图是“高大”的?
查看答案和解析>>
科目:gzsx
来源:江苏期末题
题型:解答题
已知椭圆C
1:

的离心率为

,一个焦点坐标为
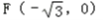
.
(1)求椭圆C
1的方程;
(2)点N是椭圆的左顶点,点P是椭圆C
1上不同于点N的任意一点,连接NP并延长交椭圆右准线与点T,求

的取值范围;
(3)设曲线
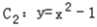
与y轴的交点为M,过M作两条互相垂直的直线与曲线C
2、椭圆C
1相交于点A、D和B、E,(如图),记△MAB、△MDE的面积分别是S
1,S
2,当

时,求直线AB的方程.
查看答案和解析>>
科目:gzsx
来源:2011-2012学年江苏省南通市如皋中学高二(上)12月月考数学试卷(解析版)
题型:解答题
已知椭圆C
1:
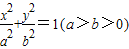
的离心率为
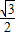
,一个焦点坐标为
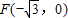
.
(1)求椭圆C
1的方程;
(2)点N是椭圆的左顶点,点P是椭圆C
1上不同于点N的任意一点,连接
NP并延长交椭圆右准线与点T,求
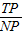
的取值范围;
(3)设曲线
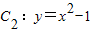
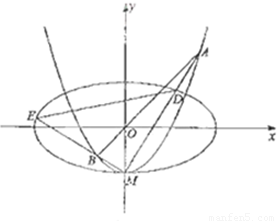
与y轴的交点为M,过M作两条互相垂直的直线与曲线C
2、椭圆C
1相交于点A、D和B、E,(如图),记△MAB、
△MDE的面积分别是S
1,S
2,当

时,求直线AB的方程.
查看答案和解析>>
科目:gzsx
来源:成功之路·突破重点线·数学(学生用书)
题型:044
如图所示,设C(a,b)是定点(ab≠0),过C作两条互相垂直的直线l1和l2,且l1,l2分别交x,y轴于A,B,求:

(1)线段AB中点M的轨迹方程;
(2)|MC|的最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:
如下图所示,是树形图形.第一层是一条与水平线垂直的线段,长度为1;第二层在第一层线段的前端作两条与该段均成135°的线段,长度为其一半;第三层按第二层的方法在每一线段的前端生成两条线段;重复前面的做法作图至第n层.设树形图的第n层的最高点到水平线的距离为第n层树形图的高度.

(1)求第三层及第四层树形图的高度H3,H4;
(2)求第n层树形图的高度Hn;
(3)若树形图的高度大于2,则称树形图为“高大”,否则称为“矮小”.显然,当n=1,2时是“矮小”的,是否存在m∈Z使得当n>m时,该树形图是“高大”的?
查看答案和解析>>

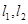 设原点到直线
设原点到直线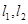 的距离分别为
的距离分别为 ,则
,则 的最大值是
。
的最大值是
。 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C. 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程; 的面积的最大值。
的面积的最大值。 作两条相互垂直的直线
作两条相互垂直的直线 ,
, 交x轴于A点,
交x轴于A点, 交y轴于B点,则线段AB的中点M的轨迹方程是( )
交y轴于B点,则线段AB的中点M的轨迹方程是( ) B.
B.
 D.
D.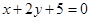
 已知椭圆C1:
已知椭圆C1:
 的离心率为
的离心率为 ,一个焦点坐标为
,一个焦点坐标为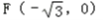 .
. 的取值范围;
的取值范围;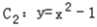 与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、△MDE的面积分别是S1,S2,当
与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、△MDE的面积分别是S1,S2,当 时,求直线AB的方程.
时,求直线AB的方程.
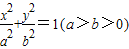 的离心率为
的离心率为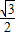 ,一个焦点坐标为
,一个焦点坐标为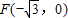 .
.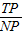 的取值范围;
的取值范围;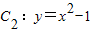 与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、
与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、 时,求直线AB的方程.
时,求直线AB的方程.

