科目:gzsx
来源:
题型:
函数
f(x)=x-,其中a为常数.
(1)证明:对任意a∈R,函数y=f(x)图象恒过定点;
(2)当a=1时,不等式f(x)+2b≤0在x∈(0,+∞)上有解,求实数b的取值范围;
(3)若对任意a∈[m,0)时,函数y=f(x)在定义域上恒单调递增,求m的最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:
下列几个命题:
(1)函数f(x)=x
n+a
x-1(n∈Z,a>0,a≠1)的图象必过点(1,2);
(2)f(x)=
+
是偶函数,但不是奇函数;
(3)函数y=f(x)值域是[-3,3],则函数y=f(x-2)值域是[-1,5];
(4)设函数y=f(x)定义域为R,则函数y=f(1-x)与y=f(x-1)图象关于y轴对称;
(5)y=|3-x
2|图象与直线y=a有k个公共点,则k的值不可能是1;
上述五个命题中所有正确的命题序号是
①④⑤
①④⑤
.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年山东省济宁市兖州市高一(上)期中数学试卷(解析版)
题型:选择题
已知函数y=f(x)的定义域为R,且对任意的x,y∈R都有f(x+y)=f(x)+f(y),则函数y=f(x)是( )
A.偶函数
B.奇函数
C.既是奇函数又是偶函数
D.非奇非偶函数
查看答案和解析>>
科目:gzsx
来源:2012-2013学年山东省济宁市兖州市高一(上)期中数学试卷(解析版)
题型:选择题
已知函数y=f(x)的定义域为R,且对任意的x,y∈R都有f(x+y)=f(x)+f(y),则函数y=f(x)是( )
A.偶函数
B.奇函数
C.既是奇函数又是偶函数
D.非奇非偶函数
查看答案和解析>>
科目:gzsx
来源:2012-2013学年江苏省常州二中高三(上)10月周末数学试卷(文科)(解析版)
题型:解答题
函数
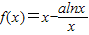
,其中a为常数.
(1)证明:对任意a∈R,函数y=f(x)图象恒过定点;
(2)当a=1时,不等式f(x)+2b≤0在x∈(0,+∞)上有解,求实数b的取值范围;
(3)若对任意a∈[m,0)时,函数y=f(x)在定义域上恒单调递增,求m的最小值.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
函数
f(x)=x-,其中a为常数.
(1)证明:对任意a∈R,函数y=f(x)图象恒过定点;
(2)当a=1时,不等式f(x)+2b≤0在x∈(0,+∞)上有解,求实数b的取值范围;
(3)若对任意a∈[m,0)时,函数y=f(x)在定义域上恒单调递增,求m的最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
函数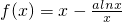 ,其中a为常数.
,其中a为常数.
(1)证明:对任意a∈R,函数y=f(x)图象恒过定点;
(2)当a=1时,不等式f(x)+2b≤0在x∈(0,+∞)上有解,求实数b的取值范围;
(3)若对任意a∈[m,0)时,函数y=f(x)在定义域上恒单调递增,求m的最小值.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年江苏省常州二中高三(上)10月周末数学试卷(文科)(解析版)
题型:解答题
函数

,其中a为常数.
(1)证明:对任意a∈R,函数y=f(x)图象恒过定点;
(2)当a=1时,不等式f(x)+2b≤0在x∈(0,+∞)上有解,求实数b的取值范围;
(3)若对任意a∈[m,0)时,函数y=f(x)在定义域上恒单调递增,求m的最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=
•(+),其中
=(coswx,0),
=(sinwx,1),且w为正实数.
(1)求f(x)的最小值;
(2)对任意m∈R,函数y=f(x),x∈[m,m+4π]的图象与直线2y+1=0有且仅有一个交点,试判断函数f(x+
)的奇偶性,并说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=
•(
-
),其中
=(cosωx,0),
=(
sinωx,1),且ω为正实数.
(1)求f(x)的最大值;
(2)对任意m∈R,函数y=f(x),x∈[m,m+π]的图象与直线y=
有且仅有一个交点,求ω的值,并求满足f(x)=
,x∈[
,
]的x的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2010•和平区一模)函数y=f(x)是定义在[a,b]上的增函数,其中a,b∈R,且0<b<-a,已知y=f(x)无零点,设F(x)=f2(x)+f2(-x),则对于函数y=F(x)有如下四种说法:①定义域是[-b,b];②最小值是0;③是偶函数;④在定义域内单调递增.其中正确的说法是( )
查看答案和解析>>
科目:gzsx
来源:
题型:
a、b、c是图象连续不断的函数y=f(x)定义域中的三个实数,且满足a<b<c,f(a)•f(b)<0,f(b)•f(c)<0.则函数y=f(x)在区间(a,c)上的零点个数为( )
查看答案和解析>>
科目:gzsx
来源:
题型:
已知定义在R上函数y=f(x)满足条件f(x)+f(x-1)=1,当x∈[0,1]时f(x)=x
2.给出以下四个命题:
(1)函数f(x)是以2为周期的函数;
(2)当x∈[1,2]时,f(x)=2x-x
2;
(3)函数f(x)为R上的偶函数;
(4)
f(-2005.5)=.
其中真命题的序号为
(1)(2)
(1)(2)
.
查看答案和解析>>
科目:gzsx
来源:
题型:
函数y=f(x)是定义在a,b上的增函数,其中a,b∈R且0<b<-a,已知y=f(x)无零点,设函数F(x)=f
2(x)+f
2(-x),则对于F(x)有以下四个说法:
①定义域是[-b,b];②是偶函数;③最小值是0;④在定义域内单调递增.
其中正确的有
①②
①②
(填入你认为正确的所有序号)
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•眉山二模)对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点,且有如下零点存在定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)•f(b<0,那么,函数y=f(x)在区间(a,b)内有零点.给出下列命题:
①若函数y=f(x)有反函数,则f(x)有且仅有一个零点;
②函数f(x)=2x
3-3x+1有3个零点;
③函数y=
和y=|log
2x|的图象的交点有且只有一个;
④设函数f(x)对x∈R都满足f(3+x)=f(3-x),且函数f(x)恰有6个不同的零点,则这6个零点的和为18;
其中所有正确命题的序号为
②④
②④
.(把所有正确命题的序号都填上)
查看答案和解析>>
科目:gzsx
来源:2012-2013学年江西省南昌二中高三(上)第一次考试数学试卷(文科)(解析版)
题型:解答题
已知函数f(x)=

•(

-

),其中

=(cosωx,0),

=(

sinωx,1),且ω为正实数.
(1)求f(x)的最大值;
(2)对任意m∈R,函数y=f(x),x∈[m,m+π]的图象与直线y=

有且仅有一个交点,求ω的值,并求满足f(x)=

,x∈[

,

]的x的值.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年江西省南昌二中高三(上)第一次考试数学试卷(文科)(解析版)
题型:解答题
已知函数f(x)=

•(

-
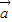
),其中

=(cosωx,0),
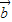
=(

sinωx,1),且ω为正实数.
(1)求f(x)的最大值;
(2)对任意m∈R,函数y=f(x),x∈[m,m+π]的图象与直线y=

有且仅有一个交点,求ω的值,并求满足f(x)=
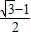
,x∈[

,
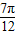
]的x的值.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年江苏省扬州市江都市大桥中学高一(下)期中数学试卷(解析版)
题型:填空题
函数y=f(x)是定义在a,b上的增函数,其中a,b∈R且0<b<-a,已知y=f(x)无零点,设函数F(x)=f2(x)+f2(-x),则对于F(x)有以下四个说法:
①定义域是[-b,b];②是偶函数;③最小值是0;④在定义域内单调递增.
其中正确的有 (填入你认为正确的所有序号)
查看答案和解析>>
科目:gzsx
来源:2010年天津市和平区高考数学一模试卷(文科)(解析版)
题型:选择题
函数y=f(x)是定义在[a,b]上的增函数,其中a,b∈R,且0<b<-a,已知y=f(x)无零点,设F(x)=f2(x)+f2(-x),则对于函数y=F(x)有如下四种说法:①定义域是[-b,b];②最小值是0;③是偶函数;④在定义域内单调递增.其中正确的说法是( )
A.①②③
B.②④
C.①③
D.①④
查看答案和解析>>
科目:gzsx
来源:2012-2013学年湖北省部分重点中学高一(上)期中数学试卷(解析版)
题型:选择题
a、b、c是图象连续不断的函数y=f(x)定义域中的三个实数,且满足a<b<c,f(a)•f(b)<0,f(b)•f(c)<0.则函数y=f(x)在区间(a,c)上的零点个数为( )
A.2
B.正的奇数
C.正的偶数
D.至少是2且至多是4
查看答案和解析>>

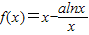 ,其中a为常数.
,其中a为常数.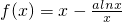 ,其中a为常数.
,其中a为常数. ,其中a为常数.
,其中a为常数. •(
•( -
- ),其中
),其中 =(cosωx,0),
=(cosωx,0), =(
=( sinωx,1),且ω为正实数.
sinωx,1),且ω为正实数. 有且仅有一个交点,求ω的值,并求满足f(x)=
有且仅有一个交点,求ω的值,并求满足f(x)= ,x∈[
,x∈[ ,
, ]的x的值.
]的x的值. •(
•( -
-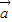 ),其中
),其中 =(cosωx,0),
=(cosωx,0),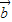 =(
=( sinωx,1),且ω为正实数.
sinωx,1),且ω为正实数. 有且仅有一个交点,求ω的值,并求满足f(x)=
有且仅有一个交点,求ω的值,并求满足f(x)=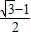 ,x∈[
,x∈[ ,
,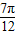 ]的x的值.
]的x的值.