练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >潜水艇上浮为正，下沉为负，若潜水艇先在距

    潜水艇上浮为正，下沉为负，若潜水艇先在距答案解析

    科目：czsx 来源： 题型：044

    潜水艇“上浮”为正，“下沉”为负，若潜水艇先在距水面78米深的A处，两次记录情况是－12米、＋18米，问潜水艇此时的位置是在A处上方还是下方？离水面的距离是多少米？

    查看答案和解析>>

    科目：czsx 来源：中华题王　数学　七年级上　(人教版) 人教版 题型：044

    潜水艇上浮为正，下沉为负，若潜水艇先在距水面80米深处，两次记录情况是－10米，20米，问潜水艇在距水面多少米的深处？

    查看答案和解析>>

    科目：czsx 来源：数学教研室 题型：044

    潜水艇“上浮”为正，“下沉”为负，若潜水艇先在距水面78米深的A处，两次记录情况是－12米、＋18米，问潜水艇此时的位置是在A处上方还是下方？离水面的距离是多少米？

    查看答案和解析>>

    科目：czsx 来源：同步题 题型：解答题

    潜水艇上浮为正，下沉为负，若潜水艇先在距水面80米深处，两次记录情况是-10米，20米，问现在潜水艇在距水面多少米的深处？

    查看答案和解析>>

    科目：czsx 来源： 题型：

    潜水艇上浮为正，下潜为负，若潜水艇先在距水面80m深处，两次记录情况是-10m，20m，问潜水艇现在在距水面多少米的深处？

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    潜水艇上浮为正，下潜为负，若潜水艇先在距水面80m深处，两次记录情况是-10m，20m，问潜水艇现在在距水面多少米的深处？

    查看答案和解析>>

    科目：czsx 来源： 题型：

    17、綦江县“三好杯”篮球运动会比赛在即，赶水中学篮球队开学后要选拔新队员充实原篮球队，按照全教练的要求：队员的标准身高为165cm．现有参选队员5人，经过体检，他们的身高分别记录为：-6cm，-4cm，+1cm，+2cm，-8cm，（高于标准身高记录为正，低于标准身高的为负）若实际选拔的队员身高为160cm-170cm，求：
    （1）这5个同学中的最高身高和最低身高各是多少？
    （2）这5个同学的平均身高是多少？
    （3）这五个同学有几人可入选该校篮球队？

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知a为正整数，b为负分数，请先化简下面的式子，再在相应的圈各选择一个适合的数代入求值：a-（2a-3b）+2（a-2b）

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    綦江县“三好杯”篮球运动会比赛在即，赶水中学篮球队开学后要选拔新队员充实原篮球队，按照全教练的要求：队员的标准身高为165cm．现有参选队员5人，经过体检，他们的身高分别记录为：-6cm，-4cm，+1cm，+2cm，-8cm，（高于标准身高记录为正，低于标准身高的为负）若实际选拔的队员身高为160cm-170cm，求：
    （1）这5个同学中的最高身高和最低身高各是多少？
    （2）这5个同学的平均身高是多少？
    （3）这五个同学有几人可入选该校篮球队？

    查看答案和解析>>

    科目：czsx 来源：不详 题型：解答题

    綦江县“三好杯”篮球运动会比赛在即，赶水中学篮球队开学后要选拔新队员充实原篮球队，按照全教练的要求：队员的标准身高为165cm．现有参选队员5人，经过体检，他们的身高分别记录为：-6cm，-4cm，+1cm，+2cm，-8cm，（高于标准身高记录为正，低于标准身高的为负）若实际选拔的队员身高为160cm-170cm，求：
    （1）这5个同学中的最高身高和最低身高各是多少？
    （2）这5个同学的平均身高是多少？
    （3）这五个同学有几人可入选该校篮球队？

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    已知a为正整数，b为负分数，请先化简下面的式子，再在相应的圈各选择一个适合的数代入求值：a-（2a-3b）+2（a-2b）

    查看答案和解析>>

    科目：czsx 来源： 题型：

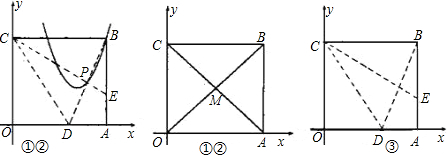
    矩形ABCD的边长AB=3，AD=2，将此矩形放在平面直角坐标系中，使AB在x轴的正精英家教网半轴上，点A在点B的左侧，另两个顶点都在第一象限，且直线y=
    32
    x-1    经过这两个顶点中的一个．
    （1）求A、B、C、D四点坐标；
    （2）以AB为直径作⊙M，记过A、B两点的抛物线y=ax2+bx+c的顶点为P．
    ①若P点在⊙M和矩形内，求a的取值范围；
    ②过点C作CF切⊙M于E，交AD于F，当PF∥AB时，求抛物线的函数解析式．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    现有四种说法：其中正确的有（　　）个
    ①几个有理数相乘，当负因数有奇数个时，积为负；
    ②若x＜0，则|x|=-x；
    ③几个有理数相乘，当积为负时，负因数有奇数个；
    ④若|x|=-x，则x＜0．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    22、已知：CD为一幢3米高的温室，其南面窗户的底框G距地面1米，CD在地面上留下的最大影长CF为2米，现欲在距C点7米的正南方A点处建一幢12米高的楼房AB（设A，C，F在同一水平线上）．
    （1）按比例较精确地作出高楼AB及它的最大影长AE；
    （2）问若大楼AB建成后是否影响温室CD的采光，试说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    在一个布口袋中装有只有颜色不同，其它都相同的白、红、黑三种颜色的小球各1只，甲乙两人进行摸球游戏；甲先从袋中摸出一球看清颜色后放回，再由乙从袋中摸出一球．
    （1）试用树状图（或列表法）表示摸球游戏所有可能的结果；
    （2）如果规定：乙摸到与甲相同颜色的球为乙胜，否则为负，试求乙在游戏中能获胜的概率．

    查看答案和解析>>

    科目：czsx 来源： 题型：

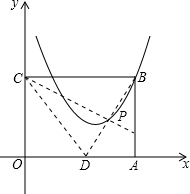
    （2012•松江区二模）已知直线y=3x-3分别与x轴、y轴交于点A，B，抛物线y=ax2+2x+c经过点A，B．
    （1）求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；
    （2）记该抛物线的对称轴为直线l，点B关于直线l的对称点为C，若点D在y轴的正半轴上，且四边形ABCD为梯形．
    ①求点D的坐标；
    ②将此抛物线向右平移，平移后抛物线的顶点为P，其对称轴与直线y=3x-3交于点E，若tan∠DPE=
    37
    ，求四边形BDEP的面积．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    （以下两小题选做一题，第1小题满分14分，第2小题满分为10分．若两小题都做，以第1小题计分）
    选做第
     
    小题．
    （1）一张矩形纸片OABC平放在平面直角坐标系内，O为原点，点A在x的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．
    ①如图，将纸片沿CE对折，点B落在x轴上的点D处，求点D的坐标；
    ②在①中，设BD与CE的交点为P，若点P，B在抛物线y=x2+bx+c上，求b，c的值；
    ③若将纸片沿直线l对折，点B落在坐标轴上的点F处，l与BF的交点为Q，若点Q在②的抛物线上，求l的解析式．
    （2）一张矩形纸片OABC平放在平面直角坐标系内，O为原点，点A在x的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．
    ①求直线AC的解析式；
    ②若M为AC与BO的交点，点M在抛物线y=-
    85
    x2+kx上，求k的值；
    ③将纸片沿CE对折，点B落在x轴上的点D处，试判断点D是否在②的抛物线上，并说明理由．精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：

    一张矩形纸片OABC平放在平面直角坐标系内，O为原点，点A在x的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．
    ①如图，将纸片沿CE对折，点B落在x轴上的点D处，求直线EC解析式；
    ②在①中，设BD与CE的交点为P，若点P，B在抛物线y=x2+bx+c上，求b，c的值；
    ③若将纸片沿直线l对折，点B落在坐标轴上的点F处，l与BF的交点为Q，若点Q在②的抛物线上，求l的解析式．精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知正n边形的中心角为60°，则n的值为
    6
    6
    ；若其边心距为
    		3
    ；则它的边长为
    2
    2
    ；面积为
    6
    		3
    6
    		3
    ．

    查看答案和解析>>

    科目：czsx 来源：第20章《二次函数和反比例函数》中考题集（46）：20.5 二次函数的一些应用（解析版） 题型：解答题

    （以下两小题选做一题，第1小题满分14分，第2小题满分为10分．若两小题都做，以第1小题计分）
    选做第______小题．
    （1）一张矩形纸片OABC平放在平面直角坐标系内，O为原点，点A在x的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．
    ①如图，将纸片沿CE对折，点B落在x轴上的点D处，求点D的坐标；
    ②在①中，设BD与CE的交点为P，若点P，B在抛物线y=x2+bx+c上，求b，c的值；
    ③若将纸片沿直线l对折，点B落在坐标轴上的点F处，l与BF的交点为Q，若点Q在②的抛物线上，求l的解析式．
    （2）一张矩形纸片OABC平放在平面直角坐标系内，O为原点，点A在x的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．
    ①求直线AC的解析式；
    ②若M为AC与BO的交点，点M在抛物线y=-x2+kx上，求k的值；
    ③将纸片沿CE对折，点B落在x轴上的点D处，试判断点D是否在②的抛物线上，并说明理由．

    查看答案和解析>>