练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知A、B两点的距离是5cm.（1）画半径为5cm的圆，使它经过

    已知A、B两点的距离是5cm.（1）画半径为5cm的圆，使它经过答案解析

    科目：czsx 来源： 题型：

    已知A，B两点之间距离是10cm，C是线段AB上任意一点，则AC的中点与BC的中点距离是（　　）
    A、3cmB、4cmC、5cmD、不能确定

    查看答案和解析>>

    科目：czsx 来源：数学教研室 题型：013

    已知A，B两点之间距离是10cm,C是线段AB上任意一点，则AC 的中点与BC的中点距离是（   ）

    （A）3cm　　    （B）4cm　　　　 （C）5cm　　    （D）不能确定

     

    查看答案和解析>>

    科目：czsx 来源：模拟题 题型：填空题

    如图，在平面直角坐标系中，矩形的两边分别在x轴和y轴上，=10，=6，P是线段OA上的动点，从O点出发，以1cm／s的速度沿方向作匀速运动，点Q在线段AB上， 已知A、Q两点间距离是O、P两点间距离的a倍，若用（a，t）表示经过时间t（s）时，△、△和△中有两个三角形全等，请写出（a，t）的所有可能情况（     ）

    查看答案和解析>>

    科目：czsx 来源：期末题 题型：单选题

    已知A，B两点之间距离是10cm，C是线段AB上任意一点，则AC的中点与BC的中点距离是
    [     ]
    A．3cm
    B．4cm
    C．5cm
    D．不能确定

    查看答案和解析>>

    科目：czsx 来源：同步题 题型：单选题

    已知A，B两点之间距离是10cm，C是线段AB上任意一点，则AC的中点与BC的中点距离是
    [     ]
    A．3cm
    B．4cm
    C．5cm
    D．不能确定

    查看答案和解析>>

    科目：czsx 来源： 题型：单选题

    已知A，B两点之间距离是10cm，C是线段AB上任意一点，则AC的中点与BC的中点距离是


    1. A.
      3cm
    2. B.
      4cm
    3. C.
      5cm
    4. D.
      不能确定

    查看答案和解析>>

    科目：czsx 来源： 题型：022

    已知矩形ABCD中，AB=8cm，BC=6cm，以A为圆心作圆，使C，D两点分别在圆的外部和圆的内部，那么⊙A的半径r的取值范围应为________．

    查看答案和解析>>

    科目：czsx 来源：数学教研室 题型：022

    已知矩形ABCD中，AB=8cm，BC=6cm，以A为圆心作圆，使C，D两点分别在圆的外部和圆的内部，那么⊙A的半径r的取值范围应为________．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    8、如图，已知点A在⊙O上，点B在⊙O外，求作一个圆，使它经过点B，并且与⊙O相切于点A．（要求写出作法，不要求证明）

    查看答案和解析>>

    科目：czsx 来源：不详 题型：解答题

    如图，已知点A在⊙O上，点B在⊙O外，求作一个圆，使它经过点B，并且与⊙O相切于点A．（要求写出作法，不要求证明）

    精英家教网

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    如图，已知点A在⊙O上，点B在⊙O外，求作一个圆，使它经过点B，并且与⊙O相切于点A．（要求写出作法，不要求证明）

    查看答案和解析>>

    科目：czsx 来源： 题型：

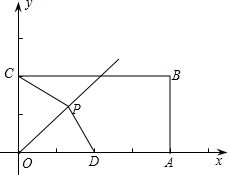
    如图，在矩形OABC中，已知A，C两点的坐标分别为A（4，0），C（0，2），点D精英家教网是OA的中点；设点P是∠AOC平分线上的一个动点（不与点O重合）．
    （1）试证明：无论点P运动到何处，PC与PD总相等；
    （2）当点P运动到与点B的距离最小时，试确定过O，P，D三点的抛物线的解析式；
    （3）设点N是矩形OABC的对称中心，是否存在点P，使∠CPN=90°？若存在，请写出P点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

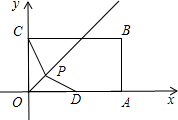
    如图，在矩形OABC中，已知A、C两点的坐标分别为A（4，0）、C（0，2），D为OA的中点．设点P是∠AOC精英家教网平分线上的一个动点（不与点O重合）．
    （1）试证明：无论点P运动到何处，PC总与PD相等；
    （2）当点P运动到与点B的距离最小时，试确定过O、P、D三点的抛物线的解析式；
    （3）设点E是（2）中所确定抛物线的顶点，当点P运动到何处时，△PDE的周长最小？求出此时点P的坐标和△PDE的周长；
    （4）设点N是矩形OABC的对称中心，是否存在点P，使∠CPN=90°？若存在，请直接写出点P的坐标．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图，在矩形OABC中，已知A，C两点的坐标分别为A（4，0），C（0，2），D为OA的中点．设点P是∠AOC平分线上的一个动点（不与点O重合）．
    （1）试证明：无论点P运动到何处，PC总与PD相等；
    （2）当点P运动到与点B的距离最小时，求P的坐标；
    （3）已知E（1，-1），当点P运动到何处时，△PDE的周长最小？求出此时点P的坐标和△PDE的周长．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    24、在数轴上有A，B两点，其中点A所对应的数是a，点B所对应的数是1．已知A，B两点的距离小于3，请你利用数轴．
    （1）写出a所满足的不等式；
    （2）数-3，0，4所对应的点到点B的距离小于3吗？

    查看答案和解析>>

    科目：czsx 来源： 题型：

    材料一：在平面直角坐标系中，如果已知A，B两点的坐标为（x1，y1）和（x2，y2），设AB=t，那么我们可以通过构造直角三角形用勾股定理得出结论：（x1-x2）2+（y1-y2）2=t2
    材料二：根据圆的定义，圆是到定点的距离等于定长的所有点的集合（其中定点为圆心，定长为半径）．如果把圆放在平面直角坐标系中，我们设圆心坐标为（a，b），半径为r，圆上任意一点的坐标为（x，y），那么我们可以根据材料一的结论得出：（x-a）2+（y-b）2=r2，这个二元二次方程我们把它定义为圆的方程．比如：以点（3，4）为圆心，4为半径的圆，我们可以用方程（x-3）2+（y-4）2=42来表示．事实上，满足这个方程的任意一个坐标（x，y），都在已知圆上．
    认真阅读以上两则材料，回答下列问题：
    （1）方程（x-7）2+（y-8）2=81表示的是以
    （7，8）
    （7，8）
    为圆心，
    9
    9
    为半径的圆的方程．
    （2）方程x2+y2-2x+2y+1=0表示的是以
    （1，-1）
    （1，-1）
    为圆心，
    1
    1
    为半径的圆的方程； 猜想：若方程x2+y2+Dx+Ey+F=0（其中D，E，F为常数）表示的是一个圆的方程，则D，E，F要满足的条件是
    D2+E2-4F＞0
    D2+E2-4F＞0
    ．
    （3）方程x2+y2=4所表示的圆上的所有点到点（3，4）的最小距离是
    3
    3
    （直接写出结果）．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图，在矩形OABC中，已知A、C两点的坐标分别为A（4，0）、C（0，2），D为OA的中点．设点这P是∠AOC平分线上的一个动点（不与点O重合）．
    （1）填空：无论点P运动到何处，PC
     
    PD（填“＞”、“＜”或“=”）；
    （2）当点P运动到与点B的距离最小时，试确定过O、P、D三点的抛物线的解析式；
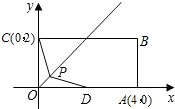
    （3）设点E是（2）中所确定抛物线的顶点，当点P运动到何处时，△PDE的周长最小？求精英家教网出此时点P的坐标和△PDE的周长．

    查看答案和解析>>

    科目：czsx 来源：第23章《二次函数与反比例函数》中考题集（30）：23.5 二次函数的应用（解析版） 题型：解答题

    如图，在矩形OABC中，已知A、C两点的坐标分别为A（4，0）、C（0，2），D为OA的中点．设点P是∠AOC平分线上的一个动点（不与点O重合）．
    （1）试证明：无论点P运动到何处，PC总与PD相等；
    （2）当点P运动到与点B的距离最小时，试确定过O、P、D三点的抛物线的解析式；
    （3）设点E是（2）中所确定抛物线的顶点，当点P运动到何处时，△PDE的周长最小？求出此时点P的坐标和△PDE的周长；
    （4）设点N是矩形OABC的对称中心，是否存在点P，使∠CPN=90°？若存在，请直接写出点P的坐标．

    查看答案和解析>>

    科目：czsx 来源：第2章《二次函数》中考题集（34）：2.8 二次函数的应用（解析版） 题型：解答题

    如图，在矩形OABC中，已知A、C两点的坐标分别为A（4，0）、C（0，2），D为OA的中点．设点P是∠AOC平分线上的一个动点（不与点O重合）．
    （1）试证明：无论点P运动到何处，PC总与PD相等；
    （2）当点P运动到与点B的距离最小时，试确定过O、P、D三点的抛物线的解析式；
    （3）设点E是（2）中所确定抛物线的顶点，当点P运动到何处时，△PDE的周长最小？求出此时点P的坐标和△PDE的周长；
    （4）设点N是矩形OABC的对称中心，是否存在点P，使∠CPN=90°？若存在，请直接写出点P的坐标．

    查看答案和解析>>

    科目：czsx 来源：2010年福建省泉州市初中毕业班数学总复习综合练习（一）（解析版） 题型：解答题

    如图，在矩形OABC中，已知A、C两点的坐标分别为A（4，0）、C（0，2），D为OA的中点．设点这P是∠AOC平分线上的一个动点（不与点O重合）．
    （1）填空：无论点P运动到何处，PC______PD（填“＞”、“＜”或“=”）；
    （2）当点P运动到与点B的距离最小时，试确定过O、P、D三点的抛物线的解析式；
    （3）设点E是（2）中所确定抛物线的顶点，当点P运动到何处时，△PDE的周长最小？求出此时点P的坐标和△PDE的周长．

    查看答案和解析>>