
科目:czsx 来源: 题型:
 4、如图,AE平分∠BAC,CE平分∠ACD,有下列条件:①∠1=∠2;②∠1+∠2=90°;③∠3+∠4=90°;④∠2+∠3=90°;其中能判定AB∥CD的有( )
4、如图,AE平分∠BAC,CE平分∠ACD,有下列条件:①∠1=∠2;②∠1+∠2=90°;③∠3+∠4=90°;④∠2+∠3=90°;其中能判定AB∥CD的有( )科目:czsx 来源:期中题 题型:解答题

科目:czsx 来源:同步练习 七年级数学 下册 题型:022
找出下面各图中的等腰三角形,并说明理由.
(1)如图,AD平分∠BAC,AD∥EC,则可得等腰三角形________,理由:________________________________;
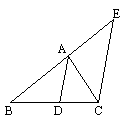
(2)如图,AE平分∠BAC,EC∥AB,则△________是等腰三角形,理由是________________________________;
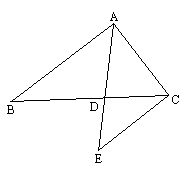
(3)如图,AD平分∠BAC,ED∥AB,则△________是等腰三角形,理由是________________________________.

从上面三题的解答中,你发现了什么规律?
科目:czsx 来源:三点一测丛书 九年级数学 上 (江苏版课标本) 江苏版课标本 题型:047
如图,△ABC内接于⊙O,AD平分∠BAC,交直线BC于点E,交⊙O于点D.
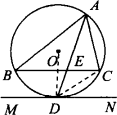
(1)过点D作MN∥BC,求证:MN是⊙O的切线;
(2)求证:AB·AC=AD·AE;
(3)如图,AE平分∠BAC的外角∠FAC,交BC的延长线于点E,EA的延长线交⊙O于点D.结论AB·AC=AD·AE是否仍然成立?如果成立,请写出证明过程;如果不成立,请说明理由.

科目:czsx 来源:数学教研室 题型:013
如图,AE平分∠BAC,CE平分∠ACD,不能判定AB∥CD的条件是
[ ]
|
A.∠1=∠2 |
B.∠1+∠2=90° |
|
C.∠3+∠4=90° |
D.∠2+∠3=90° |

科目:czsx 来源: 题型:013
如图,AE平分∠BAC,CE平分∠ACD,不能判定AB∥CD的条件是
[ ]
|
A.∠1=∠2 |
B.∠1+∠2=90° |
|
C.∠3+∠4=90° |
D.∠2+∠3=90° |

科目:czsx 来源: 题型:单选题
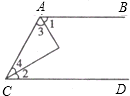 如图,AE平分∠BAC,CE平分∠ACD,不能判定AB∥CD的条件是
如图,AE平分∠BAC,CE平分∠ACD,不能判定AB∥CD的条件是科目:czsx 来源:山东省期末题 题型:单选题

科目:czsx 来源: 题型:单选题
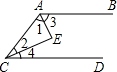 如图,AE平分∠BAC,CE平分∠ACD,有下列条件:①∠1=∠2;②∠1+∠2=90°;③∠3+∠4=90°;④∠2+∠3=90°;其中能判定AB∥CD的有
如图,AE平分∠BAC,CE平分∠ACD,有下列条件:①∠1=∠2;②∠1+∠2=90°;③∠3+∠4=90°;④∠2+∠3=90°;其中能判定AB∥CD的有科目:czsx 来源: 题型:
 我们知道,利用三角形全等可以证明两条线段相等.但是我们会碰到这样的“和差”问题:“如图①,AD为△ABC的高,∠ABC=2∠C,证明:CD=AB+BD”.我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题:在CD上截取DE=BD,连结AE.
我们知道,利用三角形全等可以证明两条线段相等.但是我们会碰到这样的“和差”问题:“如图①,AD为△ABC的高,∠ABC=2∠C,证明:CD=AB+BD”.我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题:在CD上截取DE=BD,连结AE.