科目：gzsx 来源： 题型：
科目：gzsx 来源：2013届江苏姜堰市高二第二学期期中理科数学试卷（解析版） 题型：填空题
有这样一段“三段论”推理，对于可导函数f(x)，大前提：如果f’(x0)=0，那么x=x0是函数f(x)的极值点；小前提：因为函数f(x)=x3在x=0处的导数值f’(0)=0，结论：所以x=0是函数f(x)=x3的极值点.以上推理中错误的原因是 错误（填大前提；小前提；结论）.
科目：gzsx 来源：2013-2014学年四川眉山市高三上学期一诊测文科数学试卷（解析版） 题型：选择题
对于以下判断：
（1）命题“已知
”，若x
2或y3，则x+y5”是真命题.
（2）设f(x)的导函数为f'(x)，若f'(x0)＝0，则x0是函数f(x)的极值点.
（3）命题“
,ex﹥0”的否定是：“
,ex﹥0”.
（4）对于函数f(x)，g(x)，f(x)
g(x)恒成立的一个充分不必要的条件是f(x)ming(x)max.
其中正确判断的个数是（ ）
A．1 B．2 C．3 D．0
科目：gzsx 来源：2013-2014学年四川眉山市高三上学期一诊测理科数学试卷（解析版） 题型：选择题
对于以下判断：
（1）命题“已知
”，若x
2或y3，则x+y5”是真命题.
（2）设f(x)的导函数为f'(x)，若f'(x0)＝0，则x0是函数f(x)的极值点.
（3）命题“
,ex﹥0”的否定是：“
,ex﹥0”.
（4）对于函数f(x)，g(x)，f(x)
g(x)恒成立的一个充分不必要的条件是f(x)ming(x)max.
其中正确判断的个数是（ ）
A．1 B．2 C．3 D．0
科目：gzsx 来源：新疆哈巴河县高级中学2011届高三上学期第一次月考理科数学试题 题型：013
已知命题甲：
(x0)＝0，命题乙：点x0是可导函数f(x)的极值点，则甲是乙的
充分而不必要条件
必要而不充分条件
充要条件
既不充分而不必要条件
科目：gzsx 来源：福建师大附中2010－2011学年高二下学期期中考试数学理科试题 题型：013
有一段“三段论”推理是这样的：对于可导函数f(x)，如果
＝0，那么x＝x0是函数f(x)的极值点，因为函数f(x)＝x3在x＝0处的导数值
＝0，所以，x＝0是函数f(x)＝x3的极值点．以上推理中
大前提错误
小前提错误
推理形式错误
结论正确
科目：gzsx 来源：山东省日照一中2011－2012学年高二下学期模块笔试(学段调研)数学文科试题 题型：013
已知f(x)是定义在R上的可导函数，则“
(x0)＝0”是“x0是f(x)的极值点”的
A．充分不必要条件
B．必要不充分条件
C．充分必要条件
D．既不充分也不必要条件
科目：gzsx 来源：2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)文科数学文科数学 题型：013
已知函数f(x)＝x3＋ax2＋bx＋c，下列结论中错误的是
A．
x0∈R，f(x0)＝0
B．函数y＝f(x)的图像是中心对称图形
C．若x0是f(x)的极小值点，则f(x)在区间(－∞，x0)单调递减
D．若x0是f(x)的极值点，则f’(x0)＝0
科目：gzsx 来源：江西省南昌一中、南昌十中2011届高三第一次联考理科数学试题 题型：044
已知函数f(x)＝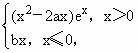
g(x)＝clnx＋b，且x＝
是函数y＝f(x)的极值点．
(Ⅰ)求实数a的值；
(Ⅱ)若方程f(x)－m＝0有两个不相等的实数根，求实数m的取值范围；
(Ⅲ)若直线l是函数y＝f(x)的图象在点(2，f(2))处的切线，且直线l与函数y＝g(x)的图象相切于点P(x0，y0)，x0∈[e－1，e]，求实数b的取值范围．
科目：gzsx 来源：河南省卫辉市第一中学2010-2011学年高二4月月考数学理科试题 题型：013
设f(x)是定义在R上的可导函数，则
(x0)＝0是x0为函数f(x)的极值点的
充分不必要条件
必要不充分条件
充要条件
既不充分也不必要条件
科目：gzsx 来源：山西省山大附中2011－2012学年高二2月月考数学理科试题 题型：013
有一段“三段论”推理是这样的：对于可导函数f(x)，如果
(x0)＝0，那么x＝x0是函数f(x)的极值点，因为函数f(x)＝x3在x＝0处的导数值
(0)＝0，所以，x＝0是函数f(x)＝x3的极值点．以上推理中
A．大前提错误
B．小前提错误
C．推理形式错误
D．结论正确
科目：gzsx 来源：2008年芜湖一中5月最后一模数学试卷(理科) 题型：022
已知函数y＝f(x)
①函数y＝f(x)在闭区间上的最大值一定是极大值．
②若
，则f(x)是以T＝6为周期的周期函数．
③若奇函数y＝f(x)在R上单调递增，那么必存在反函数y＝f－1(x)，且反函数也是奇函数，单调递增的．
④若y＝f(x)是定义在R上的可导函数，且
＝0，则x0必定是f(x)的极值点．
⑤若f(x)是奇函数，则f(0)＝0一定成立．
以上结论中错误的是________．
科目：gzsx 来源：山西省山大附中2011－2012学年高二2月月考数学文科试题 题型：013
有一段“三段论”推理是这样的：对于可导函数f(x)，如果
(x0)＝0，那么x＝x0是函数f(x)的极值点，因为函数f(x)＝x3在x＝0处的导数值
(0)＝0，所以，x＝0是函数f(x)＝x3的极值点．以上推理中
A．大前提错误
B．小前提错误
C．推理形式错误
D．结论正确
科目：gzsx 来源：四川省南山中学2011－2012学年高二五月月考数学文科试题 题型：013
设f(x)是定义在R上的可导函数，则
(x0)＝0是x0为函数f(x)的极值点的
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
科目：gzsx 来源：广东省佛山市南海一中2006－2007学年度第一学期高三数学(文科)周练14 题型：038
给出下面四个命题：
(1)若f(x)＝10，则f′(x)＝0；
(2)若x0为f(x)的极值点，则有f′(x0)＝0；
(3)若y＝f(x)在给定的区间Ａ上f′(x)＞0，则在区间A上f(x)单调递增；
(4)若f(x)＝tanx，则
其中正确的命题是________(将所有正确的命题的序号都填在横线上)
科目：gzsx 来源： 题型：
A.必有f′(x0)=0 B.f′(x0)的导数不存在
C.f′(x0)=0或f′(x0)不存在 D.f′(x0)存在但可能不为0
科目：gzsx 来源： 题型：
有一段“三段论”推理是这样的：对于可导函数f(x)，如果f’(x0)=0，那么x=x0是函数f(x)的极值点，因为函数f(x)=x3在x=0处的导数值f’(0)=0，所以x=0是函数f(x)=x3的极值点. 以上推理中（ ▲ ）
A.大前提错误 B.小前提错误 C.推理形式错误 D.结论正确
科目：gzsx 来源： 题型：填空题
科目：gzsx 来源： 题型：
已知函数f（x）=x3+ax2+bx+c ，下列结论中错误的是
（A）
（B）函数y=f（x）的图像是中心对称图形
（C）若x0是f（x）的极小值点，则f（x）在区间（-∞，x0）单调递减
（D）若x0是f(x)的极值点，则f’（ x0）=0
科目：gzsx 来源：广东省汕头市金山中学2011－2012学年高二3月月考数学文科试题 题型：044
已知函数f(x)＝(x2－2ax)ex，g(x)＝clnx＋b，
是函数y＝f(x)的极值点，其中e是自然对数的底数．
(Ⅰ)求实数a的值；
(Ⅱ)直线l同时满足：
①l是函数y＝f(x)的图象在点(2，f(2))处的切线，
②l与函数y＝g(x)的图象相切于点P(x0，y0)，x0∈[e－1，e]．
求实数b的取值范围．