
科目:czsx 来源: 题型:044
物体自由下落,开始落下时物体的高度h(m)与落到地面所用的时间t(s)之间有关系; .如果4个苹果分别从离地面2m、2.5m、3m、3.2m处落下,求它们落在地面所用时间的总和.
.如果4个苹果分别从离地面2m、2.5m、3m、3.2m处落下,求它们落在地面所用时间的总和.

科目:czsx 来源:精编教材全解 数学 九年级上册 (配苏科版) 苏科版 题型:044
一个物体从高处自由下落,落到地面所用的时间t(单位:s)与开始下落时的高度h(单位:m)有下面的关系:![]() .现有一物体从250 m的高处自由下落,则该物体落到地面所需的时间大约为多少?
.现有一物体从250 m的高处自由下落,则该物体落到地面所需的时间大约为多少?
科目:czsx 来源:101网校同步练习 初三数学 北师大(新课标2001/3年初审) 北师大版 题型:044
如图(3),在数学课题学习活动中,初三(一)班四个学习小组测量学校教学楼MN的高度.四个小组测得四组数据,制成了仪器P到楼底N的距离NP,测量仪器的高PB的数据情况的条形统计图(如图(1))和仰角情况的折线统计图(如图(2)).请你利用两个统计图提供的信息解决下列问题:


(1)把统计图中的相关数据填入下表中:

(2)求出测得的样本平均数,并根据样本平均数计算出楼高.(结果精确到0.1 m)(可能用到的数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.840.)
科目:czsx 来源: 题型:
 C、CD、DA的方向滚动,其终点分别是B、C、D、A.
C、CD、DA的方向滚动,其终点分别是B、C、D、A.科目:czsx 来源:2011-2012学年山东威海市八年级下期末模拟数学试卷(三)(带解析) 题型:解答题
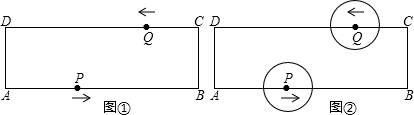
P、Q、R、S四个小球分别从正方形ABCD的四个定点A、B、C、D点出发,以同样的速度分别沿AB、BC、CD、DA的方向滚动,其终点分别是B、C、D、A。
(1)不管滚动多长时间,求证:四边形PQRS为正方形;
(2)连结对角线AC、BD、PR、SQ,你发现四条对角线有何关系?
(3)根据此图,若有四个全等的直角三角形,你能否拼成一个正方形?若这个三角形直角边为a、b,斜边问c,你能否根据面积推导出勾股定理?
科目:czsx 来源:2013届山东威海市八年级下期末模拟数学试卷(三)(解析版) 题型:解答题
P、Q、R、S四个小球分别从正方形ABCD的四个定点A、B、C、D点出发,以同样的速度分别沿AB、BC、CD、DA的方向滚动,其终点分别是B、C、D、A。

(1)不管滚动多长时间,求证:四边形PQRS为正方形;
(2)连结对角线AC、BD、PR、SQ,你发现四条对角线有何关系?
(3)根据此图,若有四个全等的直角三角形,你能否拼成一个正方形?若这个三角形直角边为a、b,斜边问c,你能否根据面积推导出勾股定理?
科目:czsx 来源: 题型:解答题
 C、CD、DA的方向滚动,其终点分别是B、C、D、A.
C、CD、DA的方向滚动,其终点分别是B、C、D、A.科目:czsx 来源:不详 题型:解答题

科目:czsx 来源: 题型:044
(1)写出h(m)与t(s)之间的函数关系式,并说明h与t的函数关系.
(2)求出物体下落2 s后,下落的高度为多少米?
(3)一个小玻璃球从高98 m的建筑物的顶端落到地面上,需要多长时间?(精确到0.1 s,![]() =2.236)
=2.236)
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:022
填空题.
物体自由下落时,它所经过的距离h(米)和时间t(秒)之间可以用关系式 来描述,建于1998年的上海金茂大厦高420.5米,当时排名世界第三高楼.若从高340米的观光厅上掉下一个物体,自由下落到地面约需________秒(精确到1秒).
来描述,建于1998年的上海金茂大厦高420.5米,当时排名世界第三高楼.若从高340米的观光厅上掉下一个物体,自由下落到地面约需________秒(精确到1秒).
科目:czsx 来源: 题型:填空题
科目:czsx 来源: 题型:
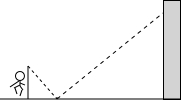 如图,王红同学跳起来把一个排球打在离她3m远的地上,然后反弹碰到墙上,如果她跳起来击球时的高度是1.8m,排球落地点离墙的距离是6m,假设球一直沿直线运动,球能碰到墙面离地( )米的地方.
如图,王红同学跳起来把一个排球打在离她3m远的地上,然后反弹碰到墙上,如果她跳起来击球时的高度是1.8m,排球落地点离墙的距离是6m,假设球一直沿直线运动,球能碰到墙面离地( )米的地方.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
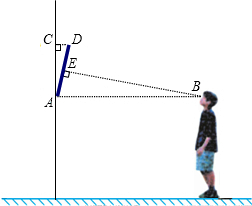 知装饰画的高度AD为0.66米,
知装饰画的高度AD为0.66米,科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
 如图,正方形ABCD的边长为10cm,点P从A开始沿折线A-D-C以2cm/s的速度移动,点Q从D开始沿CD边以1cm/s的速度移动,如果点P、Q分别从A、D同时出发,当其中一点到达C时,另一点也随之停止运动.设运动时间为t(s).
如图,正方形ABCD的边长为10cm,点P从A开始沿折线A-D-C以2cm/s的速度移动,点Q从D开始沿CD边以1cm/s的速度移动,如果点P、Q分别从A、D同时出发,当其中一点到达C时,另一点也随之停止运动.设运动时间为t(s).| 1 | 4 |
科目:czsx 来源: 题型:
 如图,在矩形ABCD中,AB=24cm,BC=8cm,点P从A开始沿折线A-B-C-D以4cm/s的速度移动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s).当t为何值时,四边形QPBC为矩形?
如图,在矩形ABCD中,AB=24cm,BC=8cm,点P从A开始沿折线A-B-C-D以4cm/s的速度移动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s).当t为何值时,四边形QPBC为矩形?科目:czsx 来源: 题型:
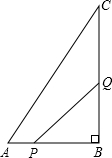 B开始沿BC边向点C以2cm/s的速度移动(点Q到达点C运动停止).如果点P,Q分别从点A,B同时出发t秒(t>0)
B开始沿BC边向点C以2cm/s的速度移动(点Q到达点C运动停止).如果点P,Q分别从点A,B同时出发t秒(t>0)科目:czsx 来源: 题型:
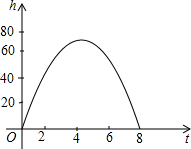 动时间t(s)的关系如图所示,求:
动时间t(s)的关系如图所示,求: