
科目:czsx 来源: 题型:
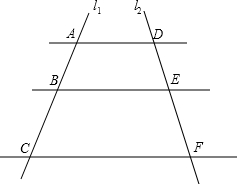 如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F.
如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F.科目:czsx 来源:2013-2014学年上海市闸北区九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,已知AD∥BE∥CF,它们依次交直线 、
、 于点A、B、C和点D、E、F,如果DE:EF=3:5,AC=24,则BC= .
于点A、B、C和点D、E、F,如果DE:EF=3:5,AC=24,则BC= .

科目:czsx 来源:2010-2011学年上海市虹口区九年级(上)期中数学试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:解答题
 如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F.
如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F.科目:czsx 来源: 题型:填空题
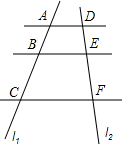 如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,如果DE:EF=3:5,AC=24,则BC=________.
如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,如果DE:EF=3:5,AC=24,则BC=________.科目:czsx 来源: 题型:
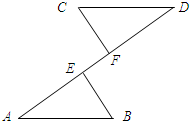 如图,已知:BE=CF,BE∥CF,AF=DE.
如图,已知:BE=CF,BE∥CF,AF=DE.科目:czsx 来源: 题型:
 填写理由或步骤
填写理由或步骤科目:czsx 来源: 题型:


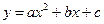 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线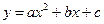 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由. 
科目:czsx 来源:2012届江苏省无锡市九年级中考模拟考试数学卷 题型:选择题
(本题满分10分)(1)探究新知:
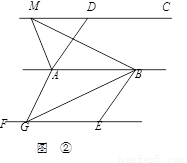
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.试判断△ABM与△ABN的面积是否相等。
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.
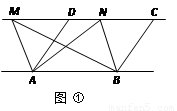

(2)结论应用:
如图③,抛物线 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.


科目:czsx 来源:2010年高级中等学校招生全国统一考试数学卷(辽宁丹东) 题型:解答题
(1)探究新知:
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.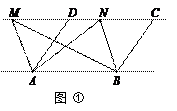
求证:△ABM与△ABN的面积相等.
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由. 
(2)结论应用:
如图③,抛物线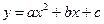 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线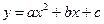 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
﹙友情提示:解答本问题过程中,可以直接使用“探究新知”中的结论.﹚ 
科目:czsx 来源:2010年高级中等学校招生全国统一考试数学卷(辽宁丹东) 题型:解答题
(1)探究新知:
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.

求证:△ABM与△ABN的面积相等.
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.
(2)结论应用:
如图③,抛物线 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等?
若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等?
若存在,请求出此时点E的坐标,若不存在,请说明理由.
﹙友情提示:解答本问题过程中,可以直接使用“探究新知”中的结论.﹚

科目:czsx 来源: 题型:
(1)探究新知:
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.

求证:△ABM与△ABN的面积相等.
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.

(2)结论应用:
如图③,抛物线的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等?若存在,请求出此时点E的坐标,若不存在,请说明理由.
﹙友情提示:解答本问题过程中,可以直接使用“探究新知”中的结论.﹚
