科目:czsx 来源: 题型:
 OB.
OB.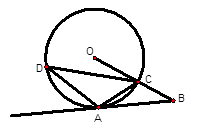
科目:czsx 来源:2011-2012学年人教版九年级第一学期期末考试数学卷 题型:解答题
(本题10分)如图,已知A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=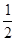 OB.
OB.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若∠ACD=45°,OC=2,求弦AD的长。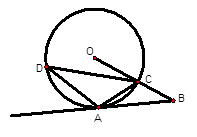
科目:czsx 来源: 题型:
(本题10分)如图,已知A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=![]() OB.
OB.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若∠ACD=45°,OC=2,求弦AD的长。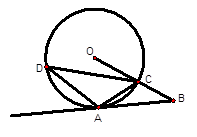
科目:czsx 来源:2012届人教版九年级第一学期期末考试数学卷 题型:选择题
(本题10分)如图,已知A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC= OB.
OB.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若∠ACD=45°,OC=2,求弦AD的长。
科目:czsx 来源: 题型:单选题
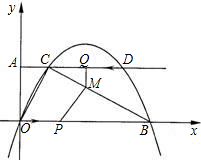
 曲线y=
曲线y=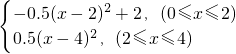 与x轴围成的面积(即图中阴影部分的面积)是多少?下面是课堂教学上同学们的看法,其中最佳答案是
与x轴围成的面积(即图中阴影部分的面积)是多少?下面是课堂教学上同学们的看法,其中最佳答案是
科目:czsx 来源: 题型:
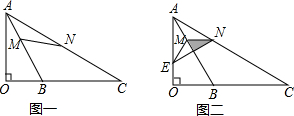
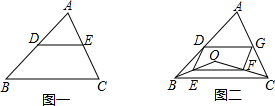 如图一,三角形ABC中,D、E分别为AB、AC的中点.
如图一,三角形ABC中,D、E分别为AB、AC的中点.科目:czsx 来源: 题型:
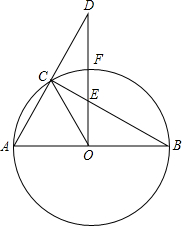 (2008•西藏)已知:如图,AB是⊙O的直径.OD⊥AB.交⊙O于点F,点C是⊙O上一点,连接OC、AC、BC.AC的延长线交OD于点D,BC交OD于点E.
(2008•西藏)已知:如图,AB是⊙O的直径.OD⊥AB.交⊙O于点F,点C是⊙O上一点,连接OC、AC、BC.AC的延长线交OD于点D,BC交OD于点E. | AF |
科目:czsx 来源: 题型:
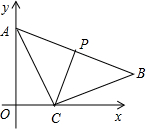
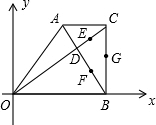 如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是点
如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是点科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
 13、
13、 (Ⅰ)已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F.
(Ⅰ)已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F.科目:czsx 来源: 题型:
 16、如图,CD是⊙O的直径,BD是弦,延长DC到A,使∠ABD=120°,若添加一个条件,使AB是⊙O的切线,则下列四个条件:①AC=BC;②AC=OC;③OC=BC;④AB=BD中,能使命题成立的有
16、如图,CD是⊙O的直径,BD是弦,延长DC到A,使∠ABD=120°,若添加一个条件,使AB是⊙O的切线,则下列四个条件:①AC=BC;②AC=OC;③OC=BC;④AB=BD中,能使命题成立的有
科目:czsx 来源: 题型:
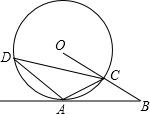 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=
已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=| 1 | 2 |
科目:czsx 来源: 题型:
 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=
已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=| 1 | 2 |
科目:czsx 来源: 题型:
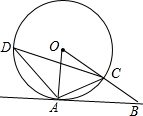 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=
已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=| 1 |
| 2 |
| 2 |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
 运动探究
运动探究科目:czsx 来源: 题型: