
科目:czsx 来源: 题型:阅读理解

科目:czsx 来源: 题型:阅读理解
| ||
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
科目:czsx 来源: 题型:阅读理解

科目:czsx 来源:2013-2014学年江苏省江阴市顾山九年级上学期期末考试数学试卷(解析版) 题型:解答题
阅读下面材料:
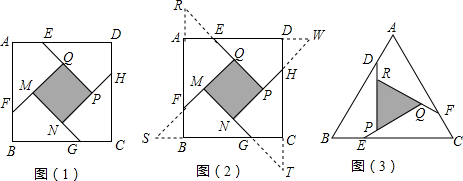
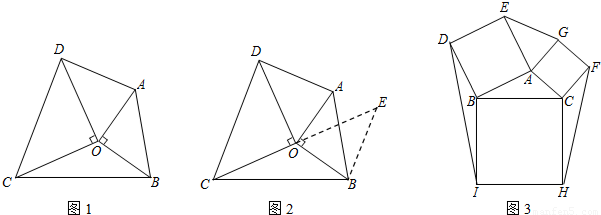
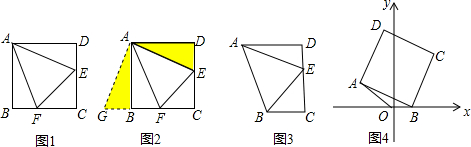
小明遇到这样一个问题:如图1,在边长为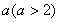 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
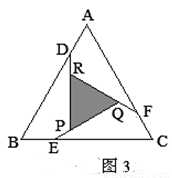
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若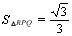 ,则AD的长为__________.
,则AD的长为__________.
科目:czsx 来源: 题型:阅读理解
阅读下面材料:
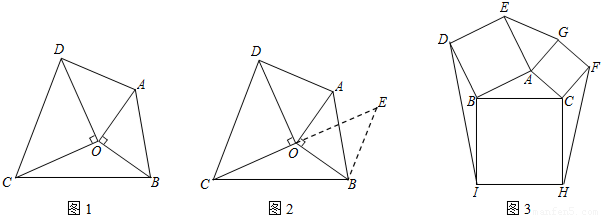
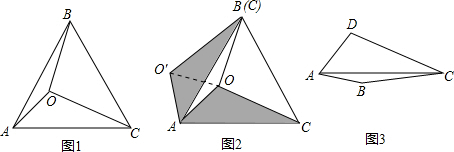
小明遇到这样一个问题:如图1,△ABO和△CDO均为等腰直角三角形, ÐAOB=ÐCOD =90°.若△BOC的面积为1, 试求以AD、BC、OC+OD的长度为三边长的三角形的面积.
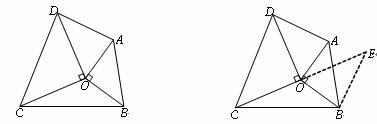
图1 图2
小明是这样思考的:要解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他利用图形变换解决了这个问题,其解题思路是延长CO到E, 使得OE=CO, 连接BE, 可证△OBE≌△OAD, 从而得到的△BCE即是以AD、BC、OC+OD的长度为三边长的三角形(如图2).
请你回答:图2中△BCE的面积等于 .
请你尝试用平移、旋转、翻折的方法,解决下列问题:
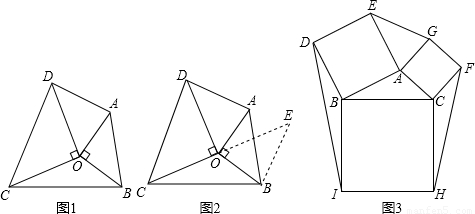
如图3,已知△ABC, 分别以AB、AC、BC为边向外作正方形ABDE、AGFC、BCHI, 连接EG、FH、ID.
(1)在图3中利用图形变换画出并指明以EG、FH、ID的长度为三边长的一个三角形(保留画图痕迹);
(2)若△ABC的面积为1,则以EG、FH、ID的长度为三边长的三角形的面积等于 .

科目:czsx 来源:2013年天津市南开区中考数学一模试卷(解析版) 题型:填空题
科目:czsx 来源:2013年北京市中考数学试卷(解析版) 题型:解答题
 ,则AD的长为______.
,则AD的长为______.
科目:czsx 来源:2012年北京市海淀区中考数学一模试卷(解析版) 题型:解答题
科目:czsx 来源: 题型:解答题

科目:czsx 来源:2012年5月中考数学模拟试卷(42)(解析版) 题型:解答题

科目:czsx 来源:2012年5月中考数学模拟试卷(25)(解析版) 题型:解答题

科目:czsx 来源:2012年河北省保定市博野县中考数学模拟试卷(解析版) 题型:解答题
科目:czsx 来源: 题型:阅读理解
阅读下面材料:
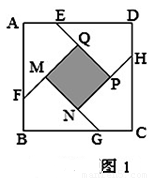
小明遇到这样一个问题:如图1,在边长为![]() 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。

小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积。
参考小明思考问题的方法,解决问题:
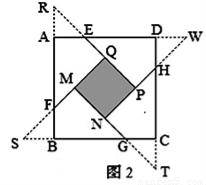
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若![]() ,则AD的长为__________。
,则AD的长为__________。
科目:czsx 来源: 题型:阅读理解
| 2 |
| 6 |
32+16
|
| 2 |
| 6 |
32+16
|
科目:czsx 来源: 题型:阅读理解
| 2 |
| 17 |
| 13 |
| 13 |
| 13 |
| 7 |
| 7 |

科目:czsx 来源: 题型:阅读理解
科目:czsx 来源:2011年初中毕业升学考试(山东临沂卷)数学解析版 题型:解答题
(2011•北京)阅读下面材料:
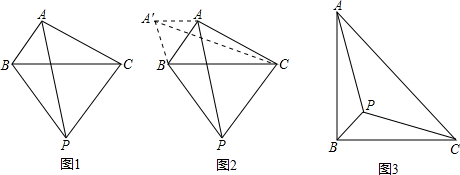
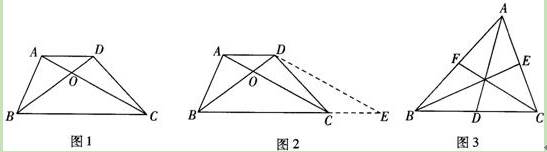
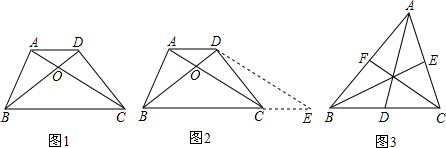
小伟遇到这样一个问题,如图1,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O.若梯形ABCD的面积为1,试求以AC,BD,AD+BC的长度为三边长的三角形的面积.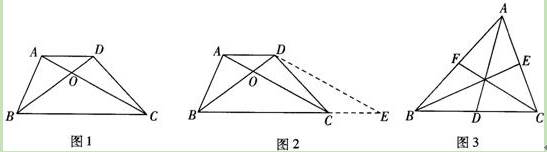
小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折,旋转,平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC,BD,AD+BC的长度为三边长的三角形(如图2).
参考小伟同学的思考问题的方法,解决下列问题:
如图3,△ABC的三条中线分别为AD,BE,CF.
(1)在图3中利用图形变换画出并指明以AD,BE,CF的长度为三边长的一个三角形(保留画图痕迹);
(2)若△ABC的面积为1,则以AD,BE,CF的长度为三边长的三角形的面积等于_____.
科目:czsx 来源: 题型:阅读理解
科目:czsx 来源: 题型:阅读理解
| 2 |
| 3 |
科目:czsx 来源: 题型:阅读理解
| 58 |
| 7 |
| 58 |
| 7 |