求证:cd⊥be答案解析

科目：czsx 来源： 题型：047

科目：czsx 来源： 题型：

如图，在梯形ABCD中，AD∥BC，∠D=90°，BE⊥AC，E为垂足，AC=BC．
（1）求证：CD=BE；
（2）若AD=3，DC=4，求AE．

科目：czsx 来源： 题型：

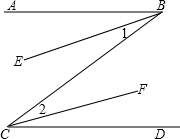已知：如图，AB∥CD，BE平分∠ABC，CF平分∠BCD．
求证：BE∥CF．
证明：∵AB∥CD（已知），
∴∠ABC=

 

（两直线平行，内错角相等），
∵BE平分∠ABC（已知），
∴∠1=

1

2

 

（角平分线的定义），
同理∠2=

1

2

 

（角平分线的定义），
∴∠1=∠2．
∴BE∥CF．

科目：czsx 来源： 题型：

23、如图所示，已知等腰梯形ABCD中，AD∥BC，AB=CD，点E为梯形外一点，且AE=DE．
求证：BE=CE．

科目：czsx 来源： 题型：

已知：如图，AB∥CD，AB=CD，AD、BC相交于点O，过点O作直线分别交AB、CD于E、F，
求证：BE=CF．

科目：czsx 来源： 题型：

（2010•绍兴）（1）如图1，在正方形ABCD中，点E，F分别在边BC，CD上，AE，BF交于点O，∠AOF=90°
求证：BE=CF．
（2）如图2，在正方形ABCD中，点E，H，F，G分别在边AB，BC，CD，DA上，EF，GH交于点O，∠FOH=90°，EF=4．则GH的长为

4

4

．
（3）已知点E，H，F，G分别在矩形ABCD的边AB，BC，CD，DA上，EF，GH交于点O，
∠FOH=90°，EF=4直接写出下列两题的答案：
①如图3，矩形ABCD由2个全等的正方形组成，则GH的长为

8

8

；

②如图4，矩形ABCD由n个全等的正方形组成，则GH的长为

4n

4n

（用n的代数式表示）

科目：czsx 来源： 题型：

23、已知：如图，CE垂直AB于E，BF垂直CD于F，且BF=CE．求证：BE=CF．

科目：czsx 来源： 题型：

某兴趣小组在学习了勾股定理之后提出：“锐（钝）角三角形有没有类似于勾股定理的结论”的问题．首先定义了一个新的概念：如图（1）△ABC中，M是BC的中点，P是射线MA上的点，设

AP

PM

=k，若∠BPC=90°，则称k为勾股比．

（1）如图（1），过B、C分别作中线AM的垂线，垂足为E、D．求证：CD=BE．
（2）①如图（2），当=1，且AB=AC时，AB²+AC²=

2.5

2.5

BC²（填一个恰当的数）．
②如图（1），当k=1，△ABC为锐角三角形，且AB≠AC时，①中的结论还成立吗？若成立，请写出证明过程；若不成立，也请说明理由；
③对任意锐角或钝角三角形，如图（1）、（3），请用含勾股比k的表达式直接表示AB²+AC²与BC²的关系（写出锐角或钝角三角形中的一个即可）．

科目：czsx 来源： 题型：

已知：如图，点E、D分别为AB、AC上一点，AD=AE，CD=BE．
求证：∠B=∠C．

科目：czsx 来源： 题型：

23、如图所示，△ABD，△ACE都是等边三角形，求证：CD=BE．

科目：czsx 来源： 题型：

已知，Rt△ABC中，∠ACB=90°，∠CAB=30°．分别以AB、AC为边，向形外作等边△ABD和等边△ACE．
（1）如图1，连接线段BE、CD．求证：BE=CD；
（2）如图2，连接DE交AB于点F．求证：F为DE中点．

科目：czsx 来源： 题型：

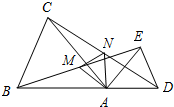已知：如图所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在同一条直线上，连接BE，CD，M，N分别为BE，CD的中点，连接AM，AN，MN．
（1）求证：BE=CD；
（2）求证：△AMN是等腰三角形．

科目：czsx 来源： 题型：

（2012•怀柔区一模）已知：如图，在四边形ABCD中，AM∥BC，E是CD中点，D是 AM上一点．求证：BE=EM．

科目：czsx 来源： 题型：

已知正方形ABCD．
（1）如图1，E是AD上一点，过BE上一点O作BE的垂线，交AB于点G，交CD于点H，求证：BE=GH；
（2）如图2，过正方形ABCD内任意一点作两条互相垂直的直线，分别交AD，BC于点E，F，交AB，CD于点G，H，EF与GH相等吗？请写出你的结论；
（3）当点O在正方形ABCD的边上或外部时，过点O作两条互相垂直的直线，被正方形相对的两边（或它们的延长线）截得的两条线段还相等吗？其中一种情形如图3所示，过正方形ABCD外一点O作互相垂直的两条直线m，n，m与AD，BC的延长线分别交于点E，F，n与AB，DC的延长线分别交于点G，H，试就该图形对你的结论加以证明．

科目：czsx 来源： 题型：

如图正方形ABCD中，点E、F分别在BC、CD上，且∠EAF=45°．
（1）求证：BE+DF=EF；
（2）若BE=3，DF=2，求AB的长．

科目：czsx 来源： 题型：

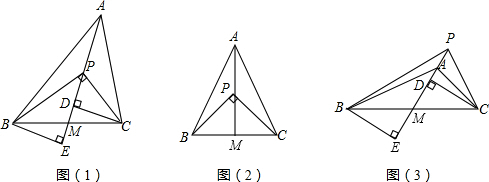
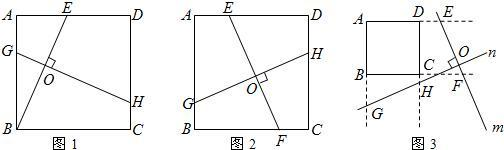
如图，在△ABC中，∠ACB=90°，D是AB的中点，过点B作∠CBE=∠A，BE与CD相交于点F，与AC相交于点E，
（1）求证：BE⊥CD；
（2）如果BE=CD，那么线段AC与BC之间具有怎样的数量关系？并证明你所得到的结论．

科目：czsx 来源： 题型：

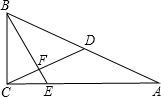
22、如图，在四边形ABCD中，E、F是对角线AC上的两点，有下面四个论断：（1）AB=CD，（2）BC=AD，（3）AE=CF，（4）BE=DF．
请用其中三个作为条件，余下一个作为结论，编一道数学题，并写出解题过程．
已知：如图，在四边形ABCD中，E、F是对角线AC上的两点，（1）AB=CD，（2）BC=AD，（3）AE=CF
求证：BE=DF
证明：

科目：czsx 来源： 题型：

（2012•昌平区一模）如图，已知△ABC和△ADE都是等边三角形，连接CD、BE．求证：CD=BE．

科目：czsx 来源： 题型：

如图，在正三角形ABC的BC边上任取一点D，以CD为边向外作正三角形CDE．求证：BE=AD．

科目：czsx 来源： 题型：

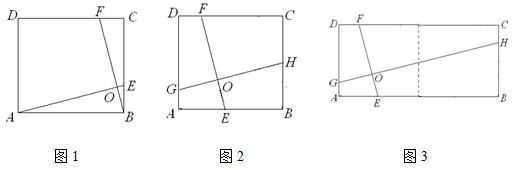
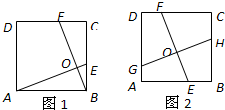23、（1）如图1，在正方形ABCD中，点E、F分别在边BC、CD上，AE、BF 交于点O，∠AOF=90°．求证：BE=CF．
（2）如图2，在正方形ABCD中，点E、H、F、G分别在边AB、BC、CD、DA上，
EF、GH交于点O，∠FOH=90°，EF=4．求GH的长．
（3）已知点E、H、F、G分别在矩形ABCD的边AB、BC、CD、DA上，EF、GH交于点O，∠FOH=90°，EF=4．直接写出下列两题的答案：
①如图3，矩形ABCD由2个全等的正方形组成，则GH=

；
②如图4，矩形ABCD由n个全等的正方形组成，则GH=

（用n的代数式表示）．