科目：czsx
来源：北京同步题
题型：填空题
若抛物线y=ax2+bx+c的系数a，b，c满足a-b+c=0，则这条抛物线必经过点（ ）。
查看答案和解析>>
科目：czsx
来源：
题型：
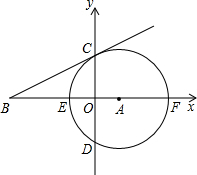
在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），⊙A与x轴交于E、F两点，与y轴交于C、D两点，过点C作⊙A的切线BC，交x轴于点B．
（1）求直线CB的解析式；
（2）若抛物线y=ax
2+bx+c的顶点在直线BC上，与x轴的交点恰为点E、F，求该抛物线的解析式；
（3）试判断点C是否在抛物线上；
（4）在抛物线上是否存在三个点，由它构成的三角形与△AOC相似？直接写出两组这样的点．
查看答案和解析>>
科目：czsx
来源：
题型：
若抛物线y=ax
2+bx+c的开口向上，且经过原点，请写出符合上述条件的一个解析式
y=x2
y=x2
．
查看答案和解析>>
科目：czsx
来源：
题型：
若抛物线y=ax
2+bx+c的顶点在第一象限，与x轴的两个交点分布在原点两侧，则点（a，
）在（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
（2012•无锡）若抛物线y=ax
2+bx+c的顶点是A（2，1），且经过点B（1，0），则抛物线的函数关系式为
y=-x2+4x-3
y=-x2+4x-3
．
查看答案和解析>>
科目：czsx
来源：
题型：
在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），与x轴交于E、F两点，与y轴交于C、D两点，过点C作⊙A的切线BC，交x轴于B．
（1）求直线CB的解析式；
（2）若抛物线y=ax
2+bx+c的顶点在直线BC上，与x轴交的点恰为⊙A与x轴的交点，求该抛物线的解析式；
（3）试判断C是否在抛物线上？
查看答案和解析>>
科目：czsx
来源：
题型：
如图①，直角坐标系中，等腰梯形OABC，AB∥OC，OA=BC，OC在x轴上，OC=7，点A的坐标为（1，3）．抛物线y=ax
2+bx+c经过O、A、C三点．
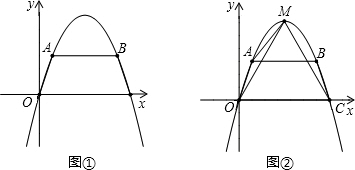
（1）求抛物线y=ax
2+bx+c的解析式并判定点B是否在抛物线上；
（2）如图②，若抛物线y=ax
2+bx+c的顶点为M，在该抛物线上点M和点C之间的曲线上确定点P，使S
△CMP=S
△OAM，求点P的坐标；
（3）若直线y=mx+n将等腰梯形OABC的周长和面积同时分成相等的两部分，请你确定y=mx+n中m的取值范围．
查看答案和解析>>
科目：czsx
来源：
题型：
在直角坐标系中，⊙A的半径为4，A的坐标为（2，0），⊙A与x轴交于E，F两点，与y轴
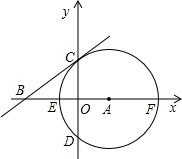
交于C、D两点，过C点作⊙A的切线BC交x轴于B
（1）求直线BC的解析式；
（2）若抛物线y=ax
2+bx+c的顶点在直线BC上，与x轴的交点恰为⊙A与x轴的交点，求抛物线的解析式；
（3）问C点是否在所求的抛物线上？
查看答案和解析>>
科目：czsx
来源：2007年全国中考数学试题汇编《二次函数》（09）（解析版）
题型：解答题
（2007•临夏州）在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），⊙A与x轴交于E、F两点，与y轴交于C、D两点，过点C作⊙A的切线BC，交x轴于点B．
（1）求直线CB的解析式；
（2）若抛物线y=ax
2+bx+c的顶点在直线BC上，与x轴的交点恰为点E、F，求该抛物线的解析式；
（3）试判断点C是否在抛物线上；
（4）在抛物线上是否存在三个点，由它构成的三角形与△AOC相似？直接写出两组这样的点．
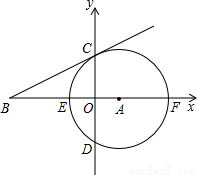
查看答案和解析>>
科目：czsx
来源：2011年江苏省泰州市泰兴实验初级中学中考数学二模试卷（解析版）
题型：解答题
如图①，直角坐标系中，等腰梯形OABC，AB∥OC，OA=BC，OC在x轴上，OC=7，点A的坐标为（1，3）．抛物线y=ax
2+bx+c经过O、A、C三点．
（1）求抛物线y=ax
2+bx+c的解析式并判定点B是否在抛物线上；
（2）如图②，若抛物线y=ax
2+bx+c的顶点为M，在该抛物线上点M和点C之间的曲线上确定点P，使S
△CMP=S
△OAM，求点P的坐标；
（3）若直线y=mx+n将等腰梯形OABC的周长和面积同时分成相等的两部分，请你确定y=mx+n中m的取值范围．
查看答案和解析>>
科目：czsx
来源：2013届江苏省大丰市第四中学九年级12月月考数学试卷（带解析）
题型：填空题
若抛物线y=ax2+bx+c的顶点是A（2，1），且经过点B（1，0），则抛物线的函数关系式为 ．
查看答案和解析>>
科目：czsx
来源：第26章《二次函数》中考题集（41）：26.3 实际问题与二次函数（解析版）
题型：解答题
在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），⊙A与x轴交于E、F两点，与y轴交于C、D两点，过点C作⊙A的切线BC，交x轴于点B．
（1）求直线CB的解析式；
（2）若抛物线y=ax
2+bx+c的顶点在直线BC上，与x轴的交点恰为点E、F，求该抛物线的解析式；
（3）试判断点C是否在抛物线上；
（4）在抛物线上是否存在三个点，由它构成的三角形与△AOC相似？直接写出两组这样的点．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
如图①，直角坐标系中，等腰梯形OABC，AB∥OC，OA=BC，OC在x轴上，OC=7，点A的坐标为（1，3）．抛物线y=ax2+bx+c经过O、A、C三点．
（1）求抛物线y=ax2+bx+c的解析式并判定点B是否在抛物线上；
（2）如图②，若抛物线y=ax2+bx+c的顶点为M，在该抛物线上点M和点C之间的曲线上确定点P，使S△CMP=S△OAM，求点P的坐标；
（3）若直线y=mx+n将等腰梯形OABC的周长和面积同时分成相等的两部分，请你确定y=mx+n中m的取值范围．
查看答案和解析>>
科目：czsx
来源：第2章《二次函数》中考题集（41）：2.4 二次函数的应用（解析版）
题型：解答题
在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），⊙A与x轴交于E、F两点，与y轴交于C、D两点，过点C作⊙A的切线BC，交x轴于点B．
（1）求直线CB的解析式；
（2）若抛物线y=ax
2+bx+c的顶点在直线BC上，与x轴的交点恰为点E、F，求该抛物线的解析式；
（3）试判断点C是否在抛物线上；
（4）在抛物线上是否存在三个点，由它构成的三角形与△AOC相似？直接写出两组这样的点．
查看答案和解析>>
科目：czsx
来源：2007年甘肃省临夏州中考数学试卷（解析版）
题型：解答题
在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），⊙A与x轴交于E、F两点，与y轴交于C、D两点，过点C作⊙A的切线BC，交x轴于点B．
（1）求直线CB的解析式；
（2）若抛物线y=ax
2+bx+c的顶点在直线BC上，与x轴的交点恰为点E、F，求该抛物线的解析式；
（3）试判断点C是否在抛物线上；
（4）在抛物线上是否存在三个点，由它构成的三角形与△AOC相似？直接写出两组这样的点．
查看答案和解析>>
科目：czsx
来源：2009年四川省攀枝花市东区中考数学二模试卷（解析版）
题型：解答题
（2007•临夏州）在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），⊙A与x轴交于E、F两点，与y轴交于C、D两点，过点C作⊙A的切线BC，交x轴于点B．
（1）求直线CB的解析式；
（2）若抛物线y=ax
2+bx+c的顶点在直线BC上，与x轴的交点恰为点E、F，求该抛物线的解析式；
（3）试判断点C是否在抛物线上；
（4）在抛物线上是否存在三个点，由它构成的三角形与△AOC相似？直接写出两组这样的点．
查看答案和解析>>
科目：czsx
来源：2010年甘肃省酒泉市三中九年级奥赛班数学选拔试卷（解析版）
题型：解答题
在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），⊙A与x轴交于E、F两点，与y轴交于C、D两点，过点C作⊙A的切线BC，交x轴于点B．
（1）求直线CB的解析式；
（2）若抛物线y=ax
2+bx+c的顶点在直线BC上，与x轴的交点恰为点E、F，求该抛物线的解析式；
（3）试判断点C是否在抛物线上；
（4）在抛物线上是否存在三个点，由它构成的三角形与△AOC相似？直接写出两组这样的点．
查看答案和解析>>
科目：czsx
来源：2012年初中毕业升学考试（江苏无锡卷）数学（解析版）
题型：填空题
若抛物线y=ax2+bx+c的顶点是A（2，1），且经过点B（1，0），则抛物线的函数关系式为 ▲ ．
查看答案和解析>>
科目：czsx
来源：2012年甘肃省中考数学仿真模拟试卷（解析版）
题型：解答题
在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），与x轴交于E、F两点，与y轴交于C、D两点，过点C作⊙A的切线BC，交x轴于B．
（1）求直线CB的解析式；
（2）若抛物线y=ax
2+bx+c的顶点在直线BC上，与x轴交的点恰为⊙A与x轴的交点，求该抛物线的解析式；
（3）试判断C是否在抛物线上？
查看答案和解析>>
科目：czsx
来源：第2章《二次函数》中考题集（44）：2.8 二次函数的应用（解析版）
题型：解答题
在直角坐标系中，⊙A的半径为4，圆心A的坐标为（2，0），⊙A与x轴交于E、F两点，与y轴交于C、D两点，过点C作⊙A的切线BC，交x轴于点B．
（1）求直线CB的解析式；
（2）若抛物线y=ax
2+bx+c的顶点在直线BC上，与x轴的交点恰为点E、F，求该抛物线的解析式；
（3）试判断点C是否在抛物线上；
（4）在抛物线上是否存在三个点，由它构成的三角形与△AOC相似？直接写出两组这样的点．
查看答案和解析>>
