科目:czsx 来源: 题型:阅读理解
【考点】菱形的性质;全等三角形的判定与性质;等边三角形的判定与性质.
【分析】根据菱形的四条边都相等,先判定△ABD是等边三角形,再根据菱形的性质可得∠BDF=∠C=60°,再求出DF=CE,然后利用“边角边”即可证明△BDF≌△DCE,从而判定①正确;根据全等三角形对应角相等可得∠DBF=∠EDC,然后利用三角形的一个外角等于与它不相邻的两个内角的和可以求出∠DMF=∠BDC=60°,再根据平角等于180°即可求出∠BMD=120°,从而判定②正确;根据三角形的一个外角等于与它不相邻的两个内角的和以及平行线的性质求出∠ABM=∠ADH,再利用“边角边”证明△ABM和△ADH全等,根据全等三角形对应边相等可得AH=AM,对应角相等可得∠BAM=∠DAH,然后求出∠MAH=∠BAD=60°,从而判定出△AMH是等边三角形,判定出③正确;根据全等三角形的面积相等可得△AMH的面积等于四边形ABMD的面积,然后判定出④错误.
【解答】在菱形ABCD中,∵AB=BD,
∴AB=BD=AD,
∴△ABD是等边三角形,
∴根据菱形的性质可得∠BDF=∠C=60°,
∵BE=CF,
∴BC-BE=CD-CF,
即CE=DF,
在△BDF和△DCE中,CE=DF;∠BDF=∠C=60°;BD=CD,
∴△BDF≌△DCE(SAS),故①小题正确;
∴∠DBF=∠EDC,
∵∠DMF=∠DBF+∠BDE=∠EDC+∠BDE=∠BDC=60°,
∴∠BMD=180°-∠DMF=180°-60°=120°,故②小题正确;
∵∠DEB=∠EDC+∠C=∠EDC+60°,∠ABM=∠ABD+∠DBF=∠DBF+60°,
∴∠DEB=∠ABM,
又∵AD∥BC,
∴∠ADH=∠DEB,
∴∠ADH=∠ABM,
在△ABM和△ADH中,AB=AD;∠ADH=∠ABM;DH=BM,
∴△ABM≌△ADH(SAS),
∴AH=AM,∠BAM=∠DAH,
∴∠MAH=∠MAD+∠DAH=∠MAD+∠BAM=∠BAD=60°,
∴△AMH是等边三角形,故③小题正确;
∵△ABM≌△ADH,
∴△AMH的面积等于四边形ABMD的面积,
又∵△AMH的面积=![]() AM·
AM·![]() AM=
AM=![]() AM2,
AM2,
∴S四边形ABMD=![]() AM2,S四边形ABCD≠S四边形ABMD,故④小题错误,
AM2,S四边形ABCD≠S四边形ABMD,故④小题错误,
综上所述,正确的是①②③共3个.
故选C.
【点评】本题考查了菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质,题目较为复杂,特别是图形的识别有难度,从图形中准确确定出全等三角形并找出全等的条件是解题的关键.
科目:czsx 来源: 题型:
 边形DEFG即为所求.
边形DEFG即为所求.科目:czsx 来源: 题型:

| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 25 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 25 |
| 1 |
| 2n |
| 5 |
| 6 |
| 11 |
| 12 |
| 23 |
| 24 |
| 47 |
| 48 |
| 95 |
| 96 |
| 191 |
| 192 |
科目:czsx 来源: 题型:
 于点E,且AB=AE.
于点E,且AB=AE.科目:czsx 来源:2011-2012学年浙江省绍兴市陶堰学区八年级上学期期中数学试卷 题型:解答题
如图,D是边长为4㎝的等边△ABC的边AB上的一点,作DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P。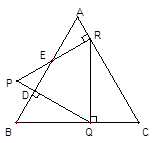
【小题1】请说明△PQR是等边三角形的理由;
【小题2】若BD=1.3㎝,则AE= ㎝(填空)
科目:czsx 来源:2011-2012学年浙江绍兴杨汛桥中学七年级下学期期中考试数学试卷(带解析) 题型:解答题
如图(1),点A、B、C在同一直线上,且△ABE, △BCD都是等边三角形,连结AD,CE.
【小题1】△BEC可由△ABD顺时针旋转得到吗?若是,请描述这一旋转变换过程;若不是,请说明理由;
【小题2】若△BCD绕点B顺时针旋转,使点A,B,C不在同一直线上(如图(2)),则在旋转过程中:
①线段AD与EC的长度相等吗?请说明理由.
②锐角 的度数是否改变?若不变,请求出
的度数是否改变?若不变,请求出 的度数;若改变,请说明理由.
的度数;若改变,请说明理由.
(注:等边三角形的三条边都相等,三个内角都是60°)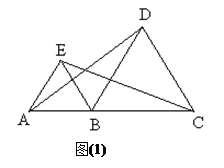

科目:czsx 来源: 题型:
 的边长为6,点
的边长为6,点 、
、 分别在边
分别在边 、
、 上,且
上,且 . 点
. 点 从点
从点 开始以每秒1个单位长的速度沿射线
开始以每秒1个单位长的速度沿射线 方向运动,设点
方向运动,设点 运动的时间为
运动的时间为 秒. 当
秒. 当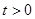 时,直线
时,直线 与过点
与过点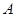 且平行于
且平行于 的直线相交于点
的直线相交于点 ,
, 的延长线与
的延长线与 的延长线相交于点
的延长线相交于点 ,
, 与
与 相交于点
相交于点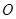
 的代数式表示
的代数式表示 ;
;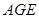 的面积为
的面积为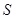 ,写出
,写出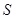 与
与 的函数关系式;
的函数关系式; 为何值时,点
为何值时,点 和点
和点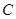 是线段
是线段 的三等分点?
的三等分点?
科目:czsx 来源: 题型:
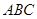 内部一点,且
内部一点,且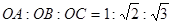 ,求
,求 的度数.
的度数.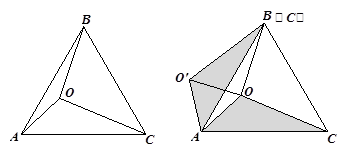
|
 绕点A逆时针旋转60°,使点C与点B重合,得到△
绕点A逆时针旋转60°,使点C与点B重合,得到△ ,连结
,连结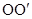 . 则△
. 则△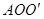 是等边三角形,故
是等边三角形,故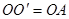 ,至此,通过旋转将线段OA、OB、OC转移到同一个三角形
,至此,通过旋转将线段OA、OB、OC转移到同一个三角形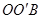 中.
中. .
.科目:czsx 来源:2012届浙江宁波北仑区中考模拟数学试卷(带解析) 题型:解答题
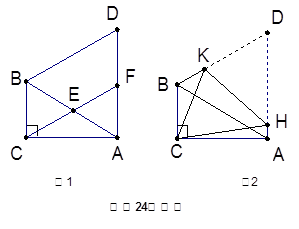
在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形
【小题1】如图1, E是AB的中点,连结CE并延长交AD于F.
求证:① △AEF≌△BEC;
② 四边形BCFD是平行四边形;
【小题2】如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,求sin∠ACH的值.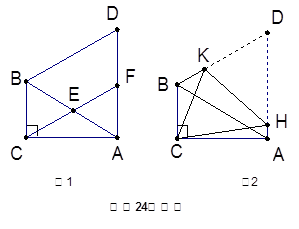
科目:czsx 来源: 题型:
科目:czsx 来源:2012届北京石景山中考二模数学试卷(带解析) 题型:解答题
小阳遇到这样一个问题:如图(1),O为等边△ 内部一点,且
内部一点,且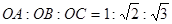 ,求
,求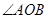 的度数.
的度数.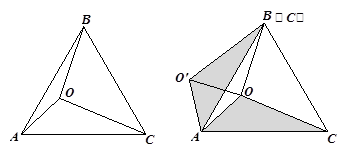
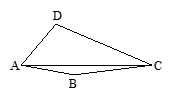
|
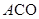 绕点A逆时针旋转60°,使点C与点B重合,得到△
绕点A逆时针旋转60°,使点C与点B重合,得到△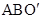 ,连结
,连结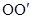 . 则△
. 则△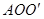 是等边三角形,故
是等边三角形,故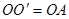 ,至此,通过旋转将线段OA、OB、OC转移到同一个三角形
,至此,通过旋转将线段OA、OB、OC转移到同一个三角形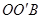 中.
中.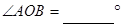 .
.科目:czsx 来源:2012届浙江省杭州市余杭瓶窑学区九年级摸底考试数学试卷(带解析) 题型:解答题
如图,已知:等边三角形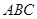 的边长为6,点
的边长为6,点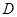 、
、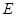 分别在边
分别在边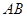 、
、 上,且
上,且 . 点
. 点 从点
从点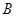 开始以每秒1个单位长的速度沿射线
开始以每秒1个单位长的速度沿射线 方向运动,设点
方向运动,设点 运动的时间为
运动的时间为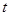 秒. 当
秒. 当 时,直线
时,直线 与过点
与过点 且平行于
且平行于 的直线相交于点
的直线相交于点 ,
, 的延长线与
的延长线与 的延长线相交于点
的延长线相交于点 ,
,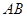 与
与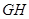 相交于点
相交于点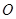
【小题1】用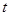 的代数式表示
的代数式表示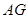 ;
;
【小题2】设△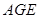 的面积为
的面积为 ,写出
,写出 与
与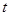 的函数关系式;
的函数关系式;
【小题3】当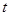 为何值时,点
为何值时,点 和点
和点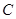 是线段
是线段 的三等分点?
的三等分点?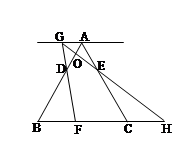
科目:czsx 来源: 题型:
 的度数是否改变?若不变,请求出
的度数是否改变?若不变,请求出 的度数;若改变,请说明理由.
的度数;若改变,请说明理由. 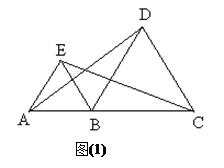

科目:czsx 来源: 题型:

科目:czsx 来源:2012年中考数学模拟试卷(六)(解析版) 题型:解答题
科目:czsx 来源:2008年湖南省益阳市中考数学试卷(解析版) 题型:解答题

科目:czsx 来源:黄冈难点课课练 八年级数学上册 题型:044
如图,四边形ABCD是菱形,△AEF是等边三角形,其中E、F分别在边BC、CD上,若等边三角形的边长与菱形的边长相等,求∠BAD的度数.

科目:czsx 来源:2009年安徽省安庆市桐城市白马中学中考数学模拟试卷(一)(解析版) 题型:解答题

科目:czsx 来源:2008年湖南省益阳市初中毕业升学统一考试、数学试卷 题型:059
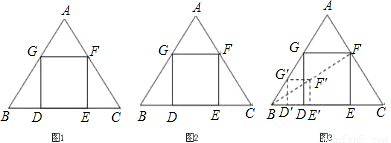
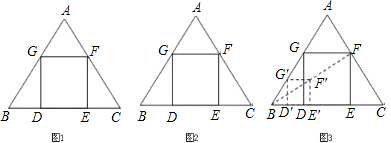
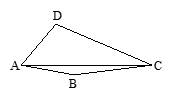
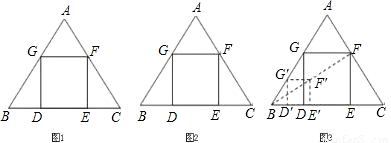
△ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.

Ⅰ.证明:△BDG≌△CEF;
Ⅱ.探究:怎样在铁片上准确地画出正方形.
小聪和小明各给出了一种想法,请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答.如果两题都解,只以Ⅱa的解答记分.
Ⅱa.小聪想:要画出正方形DEFG,只要能计算出正方形的边长就能求出BD和CE的长,从而确定D点和E点,再画正方形DEFG就容易了.
设△ABC的边长为2,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化).

Ⅱb.小明想:不求正方形的边长也能画出正方形.具体作法是:
①在AB边上任取一点![]() ,如图作正方形
,如图作正方形![]() ;
;
②连结B![]() 并延长交AC于F;
并延长交AC于F;
③作FE∥![]() 交BC于E,FG∥
交BC于E,FG∥![]() 交AB于G,GD∥
交AB于G,GD∥![]() 交BC于D,则四边形DEFG即为所求.
交BC于D,则四边形DEFG即为所求.
你认为小明的作法正确吗?说明理由.

科目:czsx 来源:2008年全国中考数学试题汇编《四边形》(07)(解析版) 题型:解答题