
科目:czsx 来源:三点一测丛书 九年级数学 上 (江苏版课标本) 江苏版课标本 题型:044
如图,以等腰直角△ABC的斜边为边向内作等边△ABD,连结DC,以DC为边作等边△DCE,B、E在CD的同侧,若AC=1,求BE长度.

科目:czsx 来源:2011-2012学年四川乐山沙湾区九年级毕业调研考试数学试卷(解析版) 题型:解答题
如图,分别以 的直角边
的直角边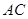 及斜边
及斜边 向外作等边
向外作等边 、等边
、等边 .若
.若 ,
, ,垂足为
,垂足为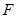 ,连结
,连结 .
.

1. ≌
≌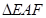
2.四边形 是平行四边形.
是平行四边形.
科目:czsx 来源:2012届四川乐山沙湾区九年级毕业调研考试数学试卷(带解析) 题型:解答题
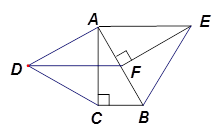
如图,分别以 的直角边
的直角边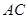 及斜边
及斜边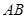 向外作等边
向外作等边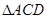 、等边
、等边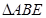 .若
.若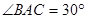 ,
, ,垂足为
,垂足为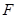 ,连结
,连结 .
.
【小题1】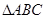 ≌
≌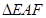
【小题2】四边形 是平行四边形.
是平行四边形.
科目:czsx 来源: 题型:
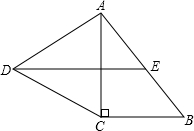 (2013•莱芜)如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(2013•莱芜)如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.科目:czsx 来源: 题型:
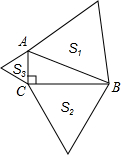 如图.在Rt△ARC中,∠ABC=90°,以Rt△ARC的三条边分别向外作等边三角形,其面积分别为S1、S2、S3,那么S1、S2、S3的关系是( )
如图.在Rt△ARC中,∠ABC=90°,以Rt△ARC的三条边分别向外作等边三角形,其面积分别为S1、S2、S3,那么S1、S2、S3的关系是( )科目:czsx 来源:2011-2012学年江苏阜宁八年级上期中调研数学试卷(解析版) 题型:解答题
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD、等边三角形ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连结DF.

①试说明AC=EF;
②求证:四边形ADFE是平行四边形.
科目:czsx 来源:2011-2012学年江苏阜宁八年级上期中调研数学试卷(带解析) 题型:解答题
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边三角形ACD、等边三角形ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连结DF.
①试说明AC=EF;
②求证:四边形ADFE是平行四边形.
科目:czsx 来源:2013年初中毕业升学考试(山东莱芜卷)数学(解析版) 题型:解答题
如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
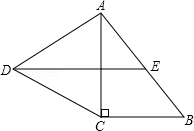
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
科目:czsx 来源:学习周报 数学 华师大八年级版 2009-2010学年 第11期 总第167期 华师大版 题型:022
如图,在Rt△ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC、AB为一边向外作等边三角形,则图中阴影部分的面积关系为________.

科目:czsx 来源:2012届北京市西城区九年级一模数学卷(解析版) 题型:解答题
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30º,EF⊥AB,垂足为F,连结DF.

(1)求证:AC=EF;
(2)求证:四边形ADFE是平行四边形.
【解析】由等边△ABE和Rt△ABC,求得Rt△ABC∽Rt△EAF,即可得AC=EF,由等边三角形的性质得出∠BDF=30°,从而证得△DBF≌△EFA,则AE=DF,再由FE=AB,得出四边形ADFE为平行四边形
科目:czsx 来源:2013年山东省莱芜市中考数学试卷(解析版) 题型:解答题
 如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.科目:czsx 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.科目:czsx 来源: 题型:
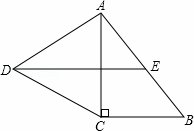
如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
科目:czsx 来源: 题型:
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30º,EF⊥AB,垂足为F,连结DF.

(1)求证:AC=EF;
(2)求证:四边形ADFE是平行四边形.
【解析】由等边△ABE和Rt△ABC,求得Rt△ABC∽Rt△EAF,即可得AC=EF,由等边三角形的性质得出∠BDF=30°,从而证得△DBF≌△EFA,则AE=DF,再由FE=AB,得出四边形ADFE为平行四边形
科目:czsx 来源:江苏省期中题 题型:证明题

科目:czsx 来源:不详 题型:单选题
| A.S2+S3=S1 | B.S2+S3>S1 |
| C.S2+S3<S1 | D.S22+S32=S12 |

科目:czsx 来源: 题型:单选题
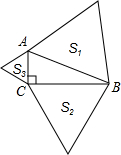 如图.在Rt△ARC中,∠ABC=90°,以Rt△ARC的三条边分别向外作等边三角形,其面积分别为S1、S2、S3,那么S1、S2、S3的关系是
如图.在Rt△ARC中,∠ABC=90°,以Rt△ARC的三条边分别向外作等边三角形,其面积分别为S1、S2、S3,那么S1、S2、S3的关系是科目:czsx 来源: 题型:
