精英家教网 >
试题搜索列表 >已知函数y=log2(-x2+2x+3) （Ⅰ）求函数的单调递增区间和最大值；求的值及函数的极值； （II）证明：当时，.时，.
已知函数y=log2(-x2+2x+3) （Ⅰ）求函数的单调递增区间和最大值；求的值及函数的极值； （II）证明：当时，.时，.答案解析
科目：gzsx
来源：
题型：
(1)已知f(x-1)=x
2-2x+3,x≤0,求f
-1(x+1).
(2)求函数f(x)=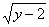
的反函数.
查看答案和解析>>
科目：gzsx
来源：
题型：
已知曲线y=
x
3+x
2+3x-3在某点处的切线斜率为2，则该点的横坐标为
．
查看答案和解析>>
科目：gzsx
来源：2011年四川省成都市新都一中高考数学一模试卷（文科）（解析版）
题型：解答题
已知曲线y=
x
3+x
2+3x-3在某点处的切线斜率为2，则该点的横坐标为
．
查看答案和解析>>
科目：gzsx
来源：2010年河南省郑州市高考数学二模试卷（文科）（解析版）
题型：解答题
已知曲线y=
x
3+x
2+3x-3在某点处的切线斜率为2，则该点的横坐标为
．
查看答案和解析>>
科目：gzsx
来源：
题型：填空题
已知曲线y=
x3+x2+3x-3在某点处的切线斜率为2，则该点的横坐标为 ________．
查看答案和解析>>
科目：gzsx
来源：0103 期末题
题型：填空题
已知曲线y=
x
3+x
2+3x-3在某点处的切线斜率为2，则该点的横坐标为（ ）。
查看答案和解析>>
科目：gzsx
来源：
题型：
已知集合
A={x|+=1}，B={x|y=x+1}，
C={y|y=log2(x2-2x+3)}（1）求∁
BA
（2）A∩C
（3）A∪C．
查看答案和解析>>
科目：gzsx
来源：
题型：
已知集合M={x|x=a
2-3a+2，a∈R}，N={
x|y=log2(x2+2x-3)}，则M∩N=
{x|x＞1}
{x|x＞1}
．
查看答案和解析>>
科目：gzsx
来源：不详
题型：填空题
已知集合M={x|x=a2-3a+2，a∈R}，N={x|y=log2(x2+2x-3)}，则M∩N=______．
查看答案和解析>>
科目：gzsx
来源：
题型：
（2012•株洲模拟）函数
y=log2(-x2+2x+3)的定义域为
{x|-1＜x＜3}
{x|-1＜x＜3}
．
查看答案和解析>>
科目：gzsx
来源：
题型：
函数
y=log2(-x2+2x+3)的单调递减区间为
．
查看答案和解析>>
科目：gzsx
来源：
题型：
函数y=
log2(x2-2x-3)的单调递增区间是
（3，+∞）
（3，+∞）
．
查看答案和解析>>
科目：gzsx
来源：
题型：
求函数y=log2(x2+2x+3)的定义域、单调区间和值域．
查看答案和解析>>
科目：gzsx
来源：
题型：
关于函数
y=log2(x2-2x+3)有以下4个结论：其中正确结论的序号是
②③④
②③④
．
①定义域（-∞，-3）∪（1，+∞）；
②递增区间[1，+∞）；
③最小值1；
④图象恒在x轴的上方．
查看答案和解析>>
科目：gzsx
来源：
题型：
已知集合A={x|-x
2+2x+3＜0}，
B={x|y=}，则A∩B=（ ）
| A、（2，3） |
| B、[2，3） |
| C、[2，+∞） |
| D、（3，+∞） |
查看答案和解析>>
科目：gzsx
来源：
题型：
函数y=log2(-x2-2x+3)的值域为（ ）
查看答案和解析>>
科目：gzsx
来源：
题型：
（2013•青岛二模）已知集合A={x|x2+2x-3＜0}，B={x|y=lg（x+2）（3-x）}．
（Ⅰ）从A∪B中任取两个不同的整数，记事件E={两个不同的整数中至少有一个是集合A∩B中的元素}，求P（E）；
（Ⅱ）从A中任取一个实数x，从B中任取一个实数y，记事件F={x与y之差的绝对值不超过1}，求P（F）．
查看答案和解析>>
科目：gzsx
来源：
题型：
下列结论：
①函数
y=和
y=()2是同一函数；
②函数f（x-1）的定义域为[1，2]，则函数f（3x
2）的定义域为
[0，]；
③函数
y=log2(x2+2x-3)的递增区间为（-1，+∞）；
④若函数f（2x-1）的最大值为3，那么f（1-2x）的最小值就是-3．
其中正确的个数为（ ）
查看答案和解析>>
科目：gzsx
来源：
题型：
求函数y=log2(x2-2x+3)的单调区间和值域．
查看答案和解析>>
科目：gzsx
来源：
题型：解答题
已知集合A={x|x2+2x-3＜0}，B={x|y=lg（x+2）（3-x）}．
（Ⅰ）从A∪B中任取两个不同的整数，记事件E={两个不同的整数中至少有一个是集合A∩B中的元素}，求P（E）；
（Ⅱ）从A中任取一个实数x，从B中任取一个实数y，记事件F={x与y之差的绝对值不超过1}，求P（F）．
查看答案和解析>>
