科目:czsx 来源: 题型:
|
科目:czsx 来源: 题型:
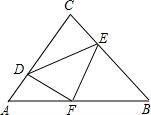 如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论:
如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论:| 1 | 2 |
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
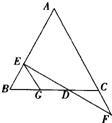
 如图:已知条件①∠1=∠2,②AD=AE,③AB=AC,④CD=BE.请选择其中的两个作为条件,得到第三个作为结论,并说明其成立的理由.(只需写一种)
如图:已知条件①∠1=∠2,②AD=AE,③AB=AC,④CD=BE.请选择其中的两个作为条件,得到第三个作为结论,并说明其成立的理由.(只需写一种)科目:czsx 来源: 题型:
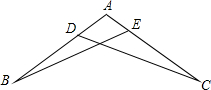
 如图,在△ABC中,∠A=α,点D、E、F分别在BC、AB、AC上.若BD=CF,CD=BE,AB=AC,则∠EDF=
如图,在△ABC中,∠A=α,点D、E、F分别在BC、AB、AC上.若BD=CF,CD=BE,AB=AC,则∠EDF=| 1 |
| 2 |
| 1 |
| 2 |
科目:czsx 来源: 题型:
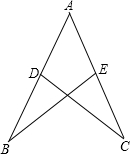 如图,点D,E分别在AB/AC上,
如图,点D,E分别在AB/AC上,科目:czsx 来源: 题型:
 如图所示,已知四边形ABCD的AB∥DC,E为AD中点,
如图所示,已知四边形ABCD的AB∥DC,E为AD中点,| 1 | 3 |
科目:czsx 来源: 题型:
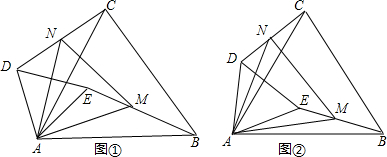
 11、如图,在△ABC中,点D、E分别在边AB、AC上.给出5个论断:
11、如图,在△ABC中,点D、E分别在边AB、AC上.给出5个论断:科目:czsx 来源: 题型:
| 3 |
科目:czsx 来源: 题型:
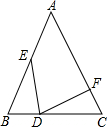
 如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE ②四边形CDFE不可能是正方形 ③△DFE是等腰直角三角形 ④S四边形CDFE=
如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE ②四边形CDFE不可能是正方形 ③△DFE是等腰直角三角形 ④S四边形CDFE=| 1 |
| 2 |
科目:czsx 来源: 题型:
 22、(A类)如图DE⊥AB,DF⊥AC,垂足分别为E,F,请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).
22、(A类)如图DE⊥AB,DF⊥AC,垂足分别为E,F,请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).