
科目:czsx 来源: 题型:阅读理解
| 3 |
| 3 |
| 3 |
| 3 |
2+
| ||
2-
|
2+
| ||
2-
|
(2+
| ||||
(2-
|
7+4
| ||
| 1 |
| 3 |
| 7 |
| 7 |
| 7 |
| 1 | ||
2+
|
| 27 |
|
| 1 | ||
1+
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
科目:czsx 来源: 题型:
| a-b | ||||
|
| a-b | ||||
|
(a-b)•(
| ||||||||
(
|
| a |
| b |
| a-b | ||||
|
(
| ||||
|
(
| ||||||||
|
| a |
| b |
| 1 | ||||
|
科目:czsx 来源: 题型:阅读理解
| 3 |
| 3 |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 | ||
|
1×
| ||||
|
| ||
| 3 |
| 1 | ||
2-
|
2+
| ||||
(2-
|
| 3 |
| 7 |
| 2 | ||
|
| 1 | ||
3
|
| 1 | ||
|
| ||
2
|
| 1 | ||
2+
|
| 27 |
|
科目:czsx 来源: 题型:
| 1 | ||
|
| ||||
|
| ||
| 3 |
| 2 | ||
|
2(
| ||||
(
|
| 3 |
| 1 | ||||
|
1•(
| ||||||||
(
|
-
| ||||
| 5 |
| ||||
|
| ||||
|
科目:czsx 来源: 题型:
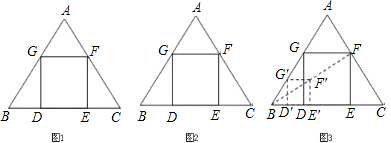 边形DEFG即为所求.
边形DEFG即为所求.科目:czsx 来源: 题型:
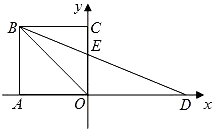 且OD=OB,BD交OC于点E.
且OD=OB,BD交OC于点E.| 2 | ||
|
2
| ||||
|
2
| ||
| 5 |
| 1 | ||
|
1×(
| ||||
(
|
| 2 |
| 1 | ||||
|
| ||||||||
(
|
| ||||
| 2 |
科目:czsx 来源:2007年广东省深圳市中考数学试卷(解析版) 题型:解答题
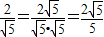 ;
;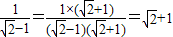 ;
;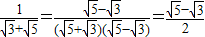 等运算都是分母有理化)
等运算都是分母有理化)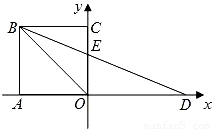
科目:czsx 来源:2011-2012学年山东省威海市八年级下学期期末数学试卷(解析版) 题型:解答题
阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如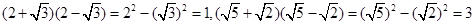 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如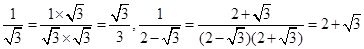 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
(1)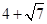 的有理化因式是
.
的有理化因式是
. 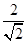 分母有理化得
.
分母有理化得
.
(2)分母有理化:(1) 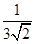 =_________;(2)
=_________;(2)
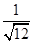 =________;(3)
=________;(3)
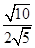 =______..
=______..
(3)计算: 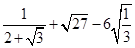 .
.
科目:czsx 来源:2012-2013学年江苏扬州江都区双沟中学九年级10月练习数学试卷(解析版) 题型:解答题
阅读材料:黑白双雄、纵横江湖;双剑合璧,天下无敌。这是武侠小说中常见的描述,其意是指两人合在一起,取长补短,威力无比。在二次根式中也有这种相辅相成的“对子”如: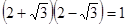 ,
,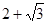 与
与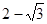 的积不含有根号,我们就说这两个式子互为有理化因式,其中一个是另一个的有理化因式。于是二次根式
的积不含有根号,我们就说这两个式子互为有理化因式,其中一个是另一个的有理化因式。于是二次根式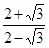 可以这样解:
可以这样解: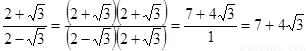 ,像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化。
,像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化。
解决问题:① 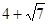 的有理化因式是_______________
的有理化因式是_______________
②计算: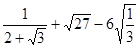
③计算: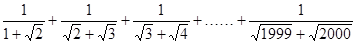
科目:czsx 来源: 题型:解答题
 且OD=OB,BD交OC于点E.
且OD=OB,BD交OC于点E.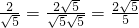 ;
;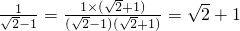 ;
;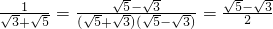 等运算都是分母有理化)
等运算都是分母有理化)科目:czsx 来源:2011-2012学年山东省威海市八年级下学期期末数学试卷(带解析) 题型:解答题
阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如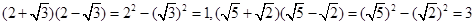 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
(1)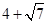 的有理化因式是 .
的有理化因式是 . 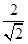 分母有理化得 .
分母有理化得 .
(2)分母有理化:(1) 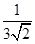 ="_________;(2)"
="_________;(2)" 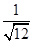 ="________;(3)"
="________;(3)" 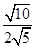 =______..
=______..
(3)计算: 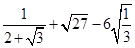 .
.
科目:czsx 来源:2011-2012学年山东威海市八年级下期末模拟数学试卷(二)(带解析) 题型:解答题
阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如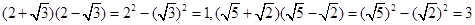 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如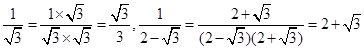 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
(1) 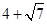 的有理化因式是 .
的有理化因式是 . 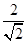 分母有理化得 .
分母有理化得 .
(2)分母有理化:(1) 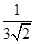 ="_________;(2)"
="_________;(2)" 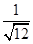 ="________;(3)"
="________;(3)" 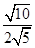 =______..
=______..
(3)计算: 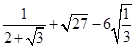 .
.
科目:czsx 来源:2013届山东威海市八年级下期末模拟数学试卷(二)(解析版) 题型:解答题
阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如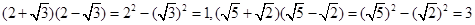 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如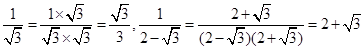 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
(1) 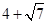 的有理化因式是
.
的有理化因式是
. 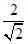 分母有理化得
.
分母有理化得
.
(2)分母有理化:(1) 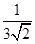 =_________;(2)
=_________;(2)
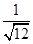 =________;(3)
=________;(3)
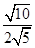 =______..
=______..
(3)计算: 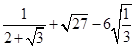 .
.
科目:czsx 来源:广东省中考真题 题型:解答题
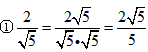 ;
;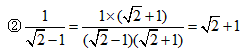 ;
;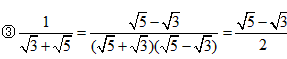 等分母有理化)
等分母有理化)
科目:czsx 来源:2007年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
 ;
;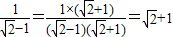 ;
;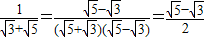 等运算都是分母有理化)
等运算都是分母有理化)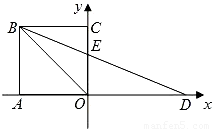
科目:czsx 来源: 题型:解答题
 ,
,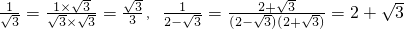 ,
,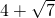 的有理化因式是______;
的有理化因式是______;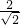 分母有理化得______.
分母有理化得______.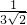 =______;②
=______;②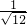 =______;③
=______;③ =______.
=______.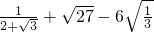 .
.科目:czsx 来源:数学教研室 题型:059
二次根式的除法运逄通常可以采用化去分母中的根号的方法来进行,例如 .数学上将这种把分母中的根号去掉的过程称作“分母有理化”,请你探索“分母有理化”的方法,并把下列各式分母有理化.
.数学上将这种把分母中的根号去掉的过程称作“分母有理化”,请你探索“分母有理化”的方法,并把下列各式分母有理化.
(1)
(2)
(3)
(4)
科目:czsx 来源:不详 题型:解答题
| a-b | ||||
|
| a-b | ||||
|
(a-b)•(
| ||||||||
(
|
| a |
| b |
| a-b | ||||
|
(
| ||||
|
(
| ||||||||
|
| a |
| b |
| 1 | ||||
|
科目:czsx 来源:2008年湖南省益阳市初中毕业升学统一考试、数学试卷 题型:059
△ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.

Ⅰ.证明:△BDG≌△CEF;
Ⅱ.探究:怎样在铁片上准确地画出正方形.
小聪和小明各给出了一种想法,请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答.如果两题都解,只以Ⅱa的解答记分.
Ⅱa.小聪想:要画出正方形DEFG,只要能计算出正方形的边长就能求出BD和CE的长,从而确定D点和E点,再画正方形DEFG就容易了.
设△ABC的边长为2,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化).

Ⅱb.小明想:不求正方形的边长也能画出正方形.具体作法是:
①在AB边上任取一点![]() ,如图作正方形
,如图作正方形![]() ;
;
②连结B![]() 并延长交AC于F;
并延长交AC于F;
③作FE∥![]() 交BC于E,FG∥
交BC于E,FG∥![]() 交AB于G,GD∥
交AB于G,GD∥![]() 交BC于D,则四边形DEFG即为所求.
交BC于D,则四边形DEFG即为所求.
你认为小明的作法正确吗?说明理由.
