精英家教网 >
试题搜索列表 >先阅读下面的材料,然后解答问题: 已知:如图1等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D. 求证:AC=AB+BD. 证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS) ∴∠AED=∠B=90°,DE=DB 又∵∠C=45°,∴△DEC是等腰直角三角形. ∴DE=EC. ∴AC=AE+EC=AB+BD. 我们将这种证明一条线段等于另两线段和的方法称为“截长法”. 解决问题:现将原题中的“AD是内角平分线,交BC边于点D”换成“A
先阅读下面的材料,然后解答问题: 已知:如图1等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D. 求证:AC=AB+BD. 证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS) ∴∠AED=∠B=90°,DE=DB 又∵∠C=45°,∴△DEC是等腰直角三角形. ∴DE=EC. ∴AC=AE+EC=AB+BD. 我们将这种证明一条线段等于另两线段和的方法称为“截长法”. 解决问题:现将原题中的“AD是内角平分线,交BC边于点D”换成“A答案解析
科目:czsx
来源:
题型:阅读理解

24、先阅读下面的材料,然后解答问题:
已知:如图1等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.
求证:AC=AB+BD.
证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS)
∴∠AED=∠B=90°,DE=DB
又∵∠C=45°,∴△DEC是等腰直角三角形.
∴DE=EC.
∴AC=AE+EC=AB+BD.
我们将这种证明一条线段等于另两线段和的方法称为“截长法”.
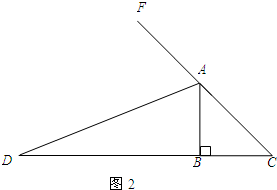
解决问题:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D,如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:czsx
来源:2011年河北省保定市中考数学一模试卷(解析版)
题型:解答题
先阅读下面的材料,然后解答问题:
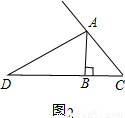
已知:如图1等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.
求证:AC=AB+BD.
证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS)
∴∠AED=∠B=90°,DE=DB
又∵∠C=45°,∴△DEC是等腰直角三角形.
∴DE=EC.
∴AC=AE+EC=AB+BD.
我们将这种证明一条线段等于另两线段和的方法称为“截长法”.
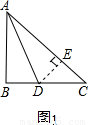
解决问题:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D,如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 先阅读下面的材料,然后解答问题:
先阅读下面的材料,然后解答问题:
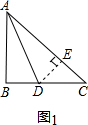
已知:如图1等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.
求证:AC=AB+BD.
证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS)
∴∠AED=∠B=90°,DE=DB
又∵∠C=45°,∴△DEC是等腰直角三角形.
∴DE=EC.
∴AC=AE+EC=AB+BD.
我们将这种证明一条线段等于另两线段和的方法称为“截长法”.
解决问题:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D,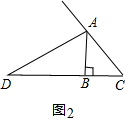 如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
先阅读下面的材料,然后解答问题:
在一条直线上有依次排列的n(n>1)台机床工作,我们要设置一个零件供应站P,使这n台机床到供应站P的距离总和最小,要解决这个问题先“退”到比较简单的情形.
如图(1),如果直线上有2台机床时,很明显设在A
1和A
2之间的任何地方都行,因为甲和乙所走的距离之和等于A
1到A
2的距离.
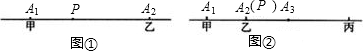
如图(2),如果直线上有3台机床时,不难判断,供应站设在中间一台机床,A
2处最合适,因为如果P不放在A
2处,甲和丙所走的距离之和恰好是A
1到A
3的距离,可是乙还得走从A
2到P的这一段,这是多出来的,因此P放在A
2处最佳选择.
不难知道,如果直线上有4台机床,P应设在第二台与第3台之间的任何地方,有5台机床,P应设在第3台位置.
问题:(1)有n台机床时,P应设在何处?
(2)根据(1)的结论,求|x-1|+|x-2|+|x-3|+…|x-617|的最小值.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
先阅读下面的材料,然后解答问题.通过计算,发现方程:
x+=2+的解为
x1=2,x2=;
x+=3+的解为
x1=3,x2=;
x+=4+的解为
x1=4,x2=;
…
(1)观察上述方程的解,猜想关于x的方程
x+=5+的解是
;
(2)根据上面的规律,猜想关于x的方程
x+=n+的解是
;
(3)类似的,关于x的方程
x-=m-的解是
;
(4)请利用上述规律求关于x的方程
=a+的解.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
先阅读下面的材料,然后解答问题:通过观察,发现方程
x+=2+的解为
x1=2,x2=;
x+=3+的解为
x1=3,x2=;
x+=4+的解为
x1=4,x2=;…
(1)观察上述方程的解,猜想关于x的方程
x+=5+的解是
;
(2)根据上面的规律,猜想关于x的方程
x+=c+的解是
;
(3)把关于x的方程
=a+变形为方程
x+=c+的形式是
没有这个
没有这个
是
,方程的解是
.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
先阅读下面的材料,然后解答问题:
①
x+=2+的解为
x1=2,x2=;
②
x+=3+的解为
x1=3,x2=;
③
x+=4+的解为
x1=4,x2=;
…
(1)观察上述方程的解的规律直接写出第④,⑤个方程及它们的解;
(2)请用一个含有正整数n的式子表示第n个方程及它的解,并用“方程的解”的概念进行验证;
(3)利用(2)的结论解关于x方程:
=a+.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
先阅读下面的材料,然后解答问题:通过观察,发现方程:
x+=2+的解为
x1=2,x2=;
x+=3+的解为
x1=3,x2=;
x+=4+的解为
x1=4,x2=;…
(1)观察上述方程的解,猜想关于x的方程
x+=5+的解是
;
(2)根据上面的规律,猜想关于x的方程
x+=c+的解是
;
(3)把关于x的方程
=a+变形为方程
x+=c+的形式是
,方程的解是
.
查看答案和解析>>
科目:czsx
来源:2014沪科版七年级上册(专题训练 状元笔记)数学:第四章 直线与角 沪科版
题型:044
先阅读下面的材料,然后解答问题:
在一条直线上有依次排列的n(n>1)台机床在工作,我们要设置零件供应站P,使这n台机床到供应站P的距离总和最小,要解决这个问题,先退到比较简单的情形:如果直线上有2台机床A1、A2时,很明显供应站P设在A1和A2之间的任何地方都行,因为甲和乙走的距离之和等于A1到A2的距离.如果直线上有3台机床A1、A2、A3时,不难判断,供应站P设在中间一台机床A2处最合适,因为如果设在A2处,甲、乙和丙所走的距离之和恰好为A1到A3的距离,若设到别处,那么甲和丙所走的距离之和仍是A1到A3的距离,可是乙还得走从A2到P这多出来的一段,故供应站P设在A2处是最佳选择.不难知道,如果直线上有4台机床,P应设在第2台与第3台之间的任何地方;有5台机床,P应设在第3台的位置.
提出问题:如果有n台机床时,供应站P应设在何处?
查看答案和解析>>
科目:czsx
来源:2004年全国中考数学试题汇编《图形认识初步》(02)(解析版)
题型:解答题
(2004•烟台)先阅读下面的材料,然后解答问题:
在一条直线上有依次排列的n(n>1)台机床工作,我们要设置一个零件供应站P,使这n台机床到供应站P的距离总和最小,要解决这个问题先“退”到比较简单的情形.
如图(1),如果直线上有2台机床时,很明显设在A
1和A
2之间的任何地方都行,因为甲和乙所走的距离之和等于A
1到A
2的距离.
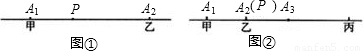
如图(2),如果直线上有3台机床时,不难判断,供应站设在中间一台机床,A
2处最合适,因为如果P不放在A
2处,甲和丙所走的距离之和恰好是A
1到A
3的距离,可是乙还得走从A
2到P的这一段,这是多出来的,因此P放在A
2处最佳选择.
不难知道,如果直线上有4台机床,P应设在第二台与第3台之间的任何地方,有5台机床,P应设在第3台位置.
问题:(1)有n台机床时,P应设在何处?
(2)根据(1)的结论,求|x-1|+|x-2|+|x-3|+…|x-617|的最小值.
查看答案和解析>>
科目:czsx
来源:2010年广东省初中毕业生学业考试数学押题卷(解析版)
题型:解答题
(2010•澄海区模拟)先阅读下面的材料,然后解答问题:通过观察,发现方程:
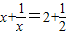
的解为
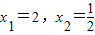
;
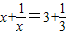
的解为
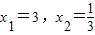
;
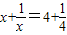
的解为
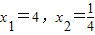
;…
(1)观察上述方程的解,猜想关于x的方程
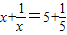
的解是______;
(2)根据上面的规律,猜想关于x的方程
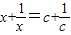
的解是______;
(3)把关于x的方程
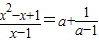
变形为方程
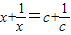
的形式是______,方程的解是______.
查看答案和解析>>
科目:czsx
来源:2010年广东省汕头市澄海区中考数学模拟试卷(解析版)
题型:解答题
(2010•澄海区模拟)先阅读下面的材料,然后解答问题:通过观察,发现方程:
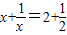
的解为
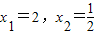
;
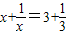
的解为
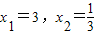
;
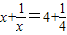
的解为
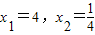
;…
(1)观察上述方程的解,猜想关于x的方程
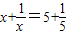
的解是______;
(2)根据上面的规律,猜想关于x的方程
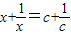
的解是______;
(3)把关于x的方程
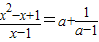
变形为方程
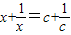
的形式是______,方程的解是______.
查看答案和解析>>
科目:czsx
来源:2013年广东省江门市福泉奥林匹克学校中考数学模拟试卷(3月份)(解析版)
题型:解答题
先阅读下面的材料,然后解答问题:通过观察,发现方程:

的解为

;

的解为

;
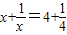
的解为

;…
(1)观察上述方程的解,猜想关于x的方程

的解是______;
(2)根据上面的规律,猜想关于x的方程

的解是______;
(3)把关于x的方程

变形为方程

的形式是______,方程的解是______.
查看答案和解析>>
科目:czsx
来源:中考必备’04全国中考试题集锦·数学
题型:044
先阅读下面的材料,然后解答问题:
在一条直线上有依次排列的n(n>1)台机床在工作,我们要设置一个零件供应站P,使这n台机床到供应站P的距离总和最小,要解决这个问题,先“退”到比较简单的情形:
如图①,如果直线上有2台机床时,很明显设在A1和A2之间的任何地方都行,因为甲和乙所走的距离之和等于A1到A2的距离.
如图②,如果直线上有3台机床时,不难判断,供应站设在中间一台机床A2处最合适.因为如果P放在A2处,甲和丙所走的距离之和恰好为A1到A3的距离.而如果把P放在别处,例如D处,那么甲和丙所走的距离之和仍是A1到A3的距离,可是乙还得走从A2到D的这一段,这是多出来的.因此P放在A2处是最佳选择.
不难知道,如果直线上有4台机床,P应设在第2台与第3台之间的任何地方;有5台机床.P应设在第3台位置.

问题(1):有n台机床时,P应设在何处?
问题(2):根据问题(1)的结论,求|x-1|+|x-2|+|x-3|+…+|x-617|的最小值.
查看答案和解析>>
科目:czsx
来源:2011-2012学年双湖中学九年级(上)月考数学试卷(解析版)
题型:解答题
先阅读下面的材料,然后解答问题.通过计算,发现方程:
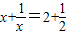
的解为

;
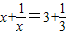
的解为
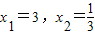
;
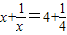
的解为
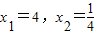
;
…
(1)观察上述方程的解,猜想关于x的方程

的解是______;
(2)根据上面的规律,猜想关于x的方程

的解是______;
(3)类似的,关于x的方程

的解是______;
(4)请利用上述规律求关于x的方程

的解.
查看答案和解析>>
科目:czsx
来源:2004年山东省烟台市中考数学试卷(解析版)
题型:解答题
(2004•烟台)先阅读下面的材料,然后解答问题:
在一条直线上有依次排列的n(n>1)台机床工作,我们要设置一个零件供应站P,使这n台机床到供应站P的距离总和最小,要解决这个问题先“退”到比较简单的情形.
如图(1),如果直线上有2台机床时,很明显设在A
1和A
2之间的任何地方都行,因为甲和乙所走的距离之和等于A
1到A
2的距离.
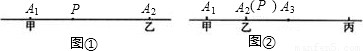
如图(2),如果直线上有3台机床时,不难判断,供应站设在中间一台机床,A
2处最合适,因为如果P不放在A
2处,甲和丙所走的距离之和恰好是A
1到A
3的距离,可是乙还得走从A
2到P的这一段,这是多出来的,因此P放在A
2处最佳选择.
不难知道,如果直线上有4台机床,P应设在第二台与第3台之间的任何地方,有5台机床,P应设在第3台位置.
问题:(1)有n台机床时,P应设在何处?
(2)根据(1)的结论,求|x-1|+|x-2|+|x-3|+…|x-617|的最小值.
查看答案和解析>>
科目:czsx
来源:月考题
题型:解答题
先阅读下面的材料,然后解答问题.通过计算,发现方程:
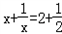
的解为
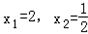
;
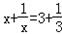
的解为

;

的解为

;
…
(1)观察上述方程的解,猜想关于x的方程

的解是
_________;
(2)根据上面的规律,猜想关于x的方程

的解是
_________;
(3)类似的,关于x的方程

的解是
_________;
(4)请利用上述规律求关于x的方程

的解.
查看答案和解析>>
科目:czsx
来源:澄海区模拟
题型:解答题
先阅读下面的材料,然后解答问题:通过观察,发现方程:
x+=2+的解为
x1=2,x2=;
x+=3+的解为
x1=3,x2=;
x+=4+的解为
x1=4,x2=;…
(1)观察上述方程的解,猜想关于x的方程
x+=5+的解是______;
(2)根据上面的规律,猜想关于x的方程
x+=c+的解是______;
(3)把关于x的方程
=a+变形为方程
x+=c+的形式是______,方程的解是______.
查看答案和解析>>

 24、先阅读下面的材料,然后解答问题:
24、先阅读下面的材料,然后解答问题:


 先阅读下面的材料,然后解答问题:
先阅读下面的材料,然后解答问题: 如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.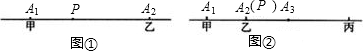
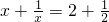 的解为
的解为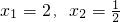 ;
;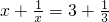 的解为
的解为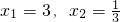 ;
;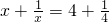 的解为
的解为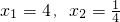 ;
;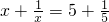 的解是______;
的解是______; 的解是______;
的解是______;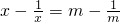 的解是______;
的解是______; 的解.
的解.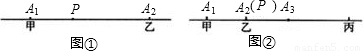
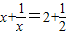 的解为
的解为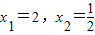 ;
;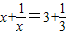 的解为
的解为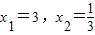 ;
;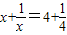 的解为
的解为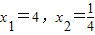 ;…
;…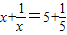 的解是______;
的解是______;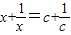 的解是______;
的解是______;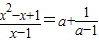 变形为方程
变形为方程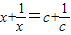 的形式是______,方程的解是______.
的形式是______,方程的解是______.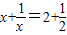 的解为
的解为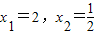 ;
;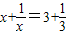 的解为
的解为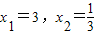 ;
;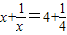 的解为
的解为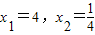 ;…
;…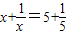 的解是______;
的解是______;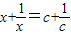 的解是______;
的解是______;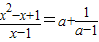 变形为方程
变形为方程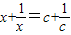 的形式是______,方程的解是______.
的形式是______,方程的解是______. 的解为
的解为 ;
; 的解为
的解为 ;
;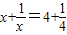 的解为
的解为 ;…
;… 的解是______;
的解是______; 的解是______;
的解是______; 变形为方程
变形为方程 的形式是______,方程的解是______.
的形式是______,方程的解是______.
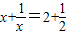 的解为
的解为 ;
;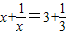 的解为
的解为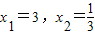 ;
;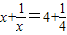 的解为
的解为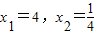 ;
; 的解是______;
的解是______; 的解是______;
的解是______; 的解是______;
的解是______; 的解.
的解.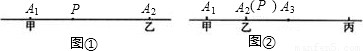
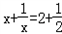 的解为
的解为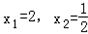 ;
;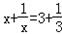 的解为
的解为 ;
; 的解为
的解为 ;
; 的解是_________;
的解是_________; 的解是_________;
的解是_________; 的解是_________;
的解是_________; 的解.
的解.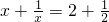 的解为
的解为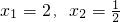 ;
;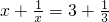 的解为
的解为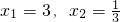 ;
;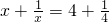 的解为
的解为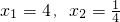 ;
; .
.