如图，△ABC中，∠C=90°，CD⊥A答案解析

科目：czsx 来源： 题型：

如图，△ABC中，∠C=90°，CD是高，已知BC=10cm，∠B=53° 6'，求CD、AC、AB（精确到1cm）．（sin53°6'=0.7997；cos53°6'=0.6004；tan53°6'=1.3319；cot53°6'=0.7508）

科目：czsx 来源： 题型：

9、如图在△ABC中，∠ACB=90°，CD⊥AB，DE⊥BC，那么与△ABC相似的三角形的个数有（　　）

A、1个

B、4个

C、3个

D、2个

科目：czsx 来源： 题型：

19、如图，△ABC中，∠ACB=90°，CD⊥AB于D，则图中所有与∠B互余的角

∠A与∠2

．

科目：czsx 来源： 题型：

如图，△ABC中，∠ACB=90°，CD是高，∠A=30°，AB=4，则BD的值为（　　）

A．3

B．2

C．1

D．l

科目：czsx 来源： 题型：

如图，△ABC中，∠ACB=90°，CD是高，∠A=30°，BD=5，则AB的长为（　　）

A．20

B．15

C．10

D．18

科目：czsx 来源： 题型：

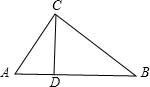如图，△ABC中，∠ACB=90°，CD⊥AB，D为垂足，若CD=6cm，AD：DB=1：2，则AD的长为（　　）

A、6cm

B、3 2 cm

C、18cm

D、3 6 cm

科目：czsx 来源： 题型：

如图，△ABC中，∠ACB=90°，CD⊥AB于D，则图中与∠1与∠B的关系成立的是（　　）

A．相等

B．互余

C．互补

D．互为对顶角

科目：czsx 来源： 题型：

如图，△ABC中，∠ACB=90°，CD、CE分别为斜边AB上的高和中线，若∠B=30°，则△ACE是

 

三角形；若AC=6，BC=8，则CD=

 

．

科目：czsx 来源： 题型：

5、如图在△ABC中，∠ACB=90°，CD⊥AB，DE⊥BC，垂足分别为D、E．则与Rt△CDE（本身除外）相似的三角形共有（　　）

A、4个

B、3个

C、2个

D、1个

科目：czsx 来源： 题型：

如图，△ABC中，∠ACB=90°，CD是斜边AB上的高，BD=9，AD=4，那么CD=

6

6

；AC=

2

13

2

13

．

科目：czsx 来源： 题型：

如图，△ABC中，∠ACB=90°，CD⊥AB于点D，若AD=6，BD=2，则BC的长是

 

．

科目：czsx 来源： 题型：

如图，△ABC中，∠ACB=90°，CD是高，∠A=30°，则BD与AB的关系是（　　）

A、BD= 1 2 AB

B、BD= 1 3 AB

C、BD= 1 4 AB

D、BD= 1 5 AB

科目：czsx 来源： 题型：

如图，△ABC中，∠ACB=90°，CD是高，∠A=30°，则AD与BD的关系是（　　）

A、AD=3BD

B、AD=2BD

C、2AD=3BD

D、AD=4BD

科目：czsx 来源： 题型：

如图，△ABC中，∠ACB=90°，CD⊥AB，∠A=30°，BD=2，则AD的长度是（　　）

A．6

B．8

C．12

D．16

科目：czsx 来源： 题型：

（2012•松北区三模）已知：如图Rt△ABC中，∠C=90°，CD是∠ACB的平分线，点M在线段AC上，点N在线段CD上．∠MND=∠ADN，NE∥BC，交BD于点E．
（1）（如图1）当点M和点A重合时，求证：AN=BE；
（2）（如图2）当MN：AD=2：3时，MC=NE，AM=2，延长MN交BC于点F，将线段BF以F为中心顺时针旋转，点B落在点P处，求出P点到BC的距离．

科目：czsx 来源： 题型：

19、如图在△ABC中，∠ACB=90°，CD是边AB上的高，AC=3，BC=4，则CD的长是

2.4

．

科目：czsx 来源： 题型：

如图，△ABC中，∠ACB=90°，CD⊥AB，点D为垂足，点E，F分别在AC．AB边上，且∠AEF=∠B．求证：EF∥CD．

科目：czsx 来源： 题型：

如图，△ABC中，∠C=90°，CD⊥AB，BD=8，AD=2，则tanA=（　　）

A．4

B．2

C． 1 2

D． 1 4

科目：czsx 来源： 题型：

17、如图，△ABC中，∠ACB=90°，CD⊥AB，则图中与△ABC（不包括△ABC）相似的三角形有

2

个．

科目：czsx 来源： 题型：

如图，△ABC中，∠C=90°，CD⊥AB，CM平分AB，CE平分∠DCM，则∠ACE的度数是

45°

45°

．