如图1,将两个完全相等的三角形纸片ABC和DEC重合放置,其中∠C=90答案解析
科目:czsx
来源:
题型:
(2013•河南)如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是
DE∥AC
DE∥AC
;
②设△BDC的面积为S
1,△AEC的面积为S
2,则S
1与S
2的数量关系是
S1=S2
S1=S2
.

(2)猜想论证
当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S
1与S
2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究
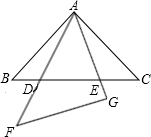
已知∠ABC=60°,点D是角平分线上一点,BD=CD=4,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S
△DCF=S
△BDE,请直接写出相应的BF的长.

查看答案和解析>>
科目:czsx
来源:2013-2014学年北京市东城区初三第一学期期末统一测试数学试卷(解析版)
题型:解答题
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90º,∠B=∠E=30º.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C顺时针旋转.当点D恰好落在AB边上时,填空:


线段DE与AC的位置关系是
;
设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是
,证明你的结论;
猜想论证
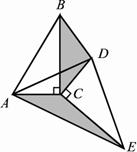
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AE中BC,CE边上的高,请你证明小明的猜想.
查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(河南卷)数学(解析版)
题型:解答题
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.
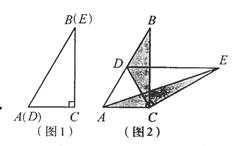

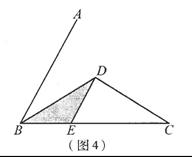
(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
②设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是 ;
②设△BDC的面积为S1,△AEC的面积为S2,那么S1,S2之间的数量关系是 ;
(2)猜想论证
 当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想;
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想;
(3)拓展探究
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE//AB交BC于点E(如图4).
 若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
查看答案和解析>>
科目:czsx
来源:2013年河南省中考数学试卷(解析版)
题型:解答题
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是______;
②设△BDC的面积为S
1,△AEC的面积为S
2,则S
1与S
2的数量关系是______.

(2)猜想论证
当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S
1与S
2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是角平分线上一点,BD=CD=4,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S
△DCF=S
△BDE,请直接写出相应的BF的长.

查看答案和解析>>
科目:czsx
来源:
题型:
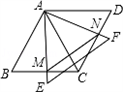
如图所示,两个同样大小的等边△ABC和△ACD,边长为12,它们拼成一个菱形ABCD,另一个足够大等边△AEF
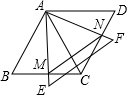
绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
(1)判断AM与AN是否相等,并简要说明理由;
(2)求四边形AMCN的面积;
(3)探索△AMN何时面积最小,并求出这个最小面积.
查看答案和解析>>
科目:czsx
来源:2011-2012学年安徽省巢湖市九年级(上)期中数学试卷(解析版)
题型:解答题
如图所示,两个同样大小的等边△ABC和△ACD,边长为12,它们拼成一个菱形ABCD,另一个足够大等边△AEF绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
(1)判断AM与AN是否相等,并简要说明理由;
(2)求四边形AMCN的面积;
(3)探索△AMN何时面积最小,并求出这个最小面积.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图所示,两个同样大小的等边△ABC和△ACD,边长为12,它们拼成一个菱形ABCD,另一个足够大等边△AEF 绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
(1)判断AM与AN是否相等,并简要说明理由;
(2)求四边形AMCN的面积;
(3)探索△AMN何时面积最小,并求出这个最小面积.
查看答案和解析>>
科目:czsx
来源:2009-2010学年安徽省巢湖市九年级(上)期中数学试卷(解析版)
题型:解答题
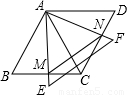
如图所示,两个同样大小的等边△ABC和△ACD,边长为12,它们拼成一个菱形ABCD,另一个足够大等边△AEF绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
(1)判断AM与AN是否相等,并简要说明理由;
(2)求四边形AMCN的面积;
(3)探索△AMN何时面积最小,并求出这个最小面积.
查看答案和解析>>
科目:czsx
来源:2008-2009学年重庆市奉节县幸福中学九年级(上)期中数学试卷(解析版)
题型:解答题
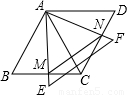
如图所示,两个同样大小的等边△ABC和△ACD,边长为12,它们拼成一个菱形ABCD,另一个足够大等边△AEF绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
(1)判断AM与AN是否相等,并简要说明理由;
(2)求四边形AMCN的面积;
(3)探索△AMN何时面积最小,并求出这个最小面积.
查看答案和解析>>
科目:czsx
来源:2010-2011学年安徽省巢湖市含山一中九年级(上)期中数学试卷(解析版)
题型:解答题
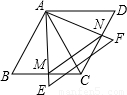
如图所示,两个同样大小的等边△ABC和△ACD,边长为12,它们拼成一个菱形ABCD,另一个足够大等边△AEF绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
(1)判断AM与AN是否相等,并简要说明理由;
(2)求四边形AMCN的面积;
(3)探索△AMN何时面积最小,并求出这个最小面积.
查看答案和解析>>
科目:czsx
来源:安徽省期中题
题型:解答题
如图所示,两个同样大小的等边△ABC和△ACD,边长为12,它们拼成一个菱形ABCD,另一个足够大等边△AEF绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
(1)判断AM与AN是否相等,并简要说明理由;
(2)求四边形AMCN的面积;
(3)探索△AMN何时面积最小,并求出这个最小面积.
查看答案和解析>>
科目:czsx
来源:
题型:
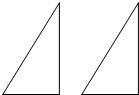
22、将两个完全相同的三角形,如图,拼在一起成为四边形,使它们有一条相等的边完全重合,则能拼出不同的平面图形( )种.
查看答案和解析>>
科目:czsx
来源:
题型:013
将两个完全相同的三角形,如图,拼在一起成为四边形,使它们有一条线等的边完全重合,则能拼出不同的平面图形( )种
A
.
2
B.
4
C.
6
D.
8
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在同一平面内,将两个全等的等腰直角△ABC和△AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,
点E不与点C重合),设BE=m,CD=n.
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对加以证明.
(2)求m与n的函数关系式,直接写出自变量n的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:

18、如图所示,两个半径相等的圆相交于A,B两点,
通过平移将两圆重合:
方法(1)
将圆O1向右平移
,
使O1与O2重合
;
方法(2)
将圆O2向左平移
,
使O2与O1重合
;
通过旋转将两圆重合:
方法(1)
将圆O1绕点B顺时针旋转,使O1与O2重合
;
方法(2)
将圆O2绕点B逆时针旋转
,
使O2与O1重合
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,将两个直角三角板的直角顶点重合在一起.

(1)若∠AOE=125°,则∠BOD=
55
55
°.
(2)若∠AOE=4∠BOD,则∠BOE=
54
54
°.
(3)将图1中的三角板DOE绕点0旋转到图2、图3的位置时,图1中∠BOD+∠AOE=
180
180
゜,图2中∠BOD+∠AOE=
180
180
°;图3中∠BOD+∠AOE=
180
180
゜,请就图2说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
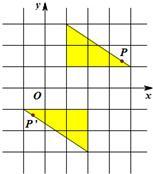
10、两个完全相同的三角形纸片,在平面直角坐标系中的摆放位置如图所示,点P与点P′是一对对应点,若点P的坐标为(a,b),则点P′的坐标为( )
查看答案和解析>>
科目:czsx
来源:
题型:
如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并且自由转动图中的转盘(转盘被分成面积相等的三角形).

如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率?试用树状图或列表法加以说明.
查看答案和解析>>
科目:czsx
来源:2011年山东省东营市学业水平模拟考试数学卷
题型:选择题
查看答案和解析>>









 当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想;
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想;
 若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.

 绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
 绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.
绕点A旋转,AE与BC相交于点M,AF与CD相交于点N.



 点E不与点C重合),设BE=m,CD=n.
点E不与点C重合),设BE=m,CD=n. 18、如图所示,两个半径相等的圆相交于A,B两点,
18、如图所示,两个半径相等的圆相交于A,B两点,

 是一对对应点,若点P的坐标为(
是一对对应点,若点P的坐标为( ,
, )则点
)则点 的坐标为( )
的坐标为( )
 ,
,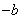 ) B. (
) B. ( ,
,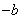 )C(
)C( ,
, ). D.(
). D.(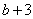 ,
, )
)