（2012?和平区一模）一块三角形废料如答案解析

科目：czsx 来源： 题型：

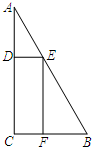（2012•和平区一模）一块三角形废料如图所示，∠A=30°，∠C=90°，AB=12．用这块废料剪出一个矩形CDEF，其中，点D、E、F分别在AC、AB、BC上．要使剪出的矩形CDEF面积最大，点E应选在何处？

科目：czsx 来源： 题型：

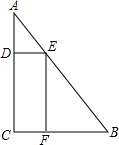（2012•道外区二模）一块三角形废料如图所示，∠A=30°，∠C=90°，AB=6米．用这块废料剪出一个矩形CDEF，其中点D、E、F分别在AC、AB、BC上、设边AE的长为x米，矩形CDEF的面积为S平方米．
（1）请直接写出S与x之间的函数关系式（不要求写出自变量x的取值范围）；
（2）根据（1）中的函数关系式，计算当x为何值时S最大，并求出最大值．
参考公式：二次函数y=ax²+bx+c（a≠0），当x=-

b

2a

时，y_{最大（小）值}=

4ac-b2

4a

．

科目：czsx 来源： 题型：

（2012•和平区一模）在平面直角坐标系中，已知点O为坐标原点，点A（0，4）．△AOB是等边三角形，点B在第一象限．
（Ⅰ）如图①，求点B的坐标；
（Ⅱ）点P是x轴上的一个动点，连接AP，以点A为旋转中心，把△AOP逆时针旋转，使边AO与AB重合，得△ABD．
①如图②，当点P运动到点（

3

，0）时，求此时点D的坐标；
②求在点P运动过程中，使△OPD的面积等于

3

4

的点P的坐标（直接写出结果即可）．

科目：czsx 来源： 题型：

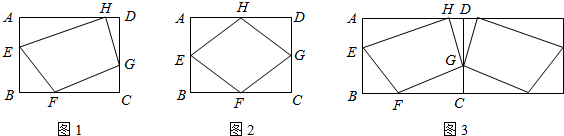
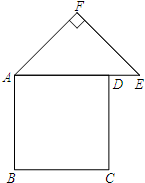（2012•和平区一模）如图，有一张纸片，是由边长为a的正方形ABCD、斜边长为2b的等腰直角三角形FAE组成的（b＜a），∠AFE=90°，且边AD和AE在同一条直线上．要通过适当的剪拼，得到一个与之面积相等的正方形．
（Ⅰ）该正方形的边长为

a2+b2

a2+b2

；
（Ⅱ）现要求只能用两条裁剪线，请你设计一种裁剪的方法，在图中画出裁剪线，并简要
说明剪拼的过程：

①在BA上截取BG=b；②画出两条裁剪线CGFG；③以点C为旋转中心，把△CBG顺时针旋转90°到△CDH的位置，以点F为旋转中心，把△FAG逆时针旋转90°到△FEH的位置．

①在BA上截取BG=b；②画出两条裁剪线CGFG；③以点C为旋转中心，把△CBG顺时针旋转90°到△CDH的位置，以点F为旋转中心，把△FAG逆时针旋转90°到△FEH的位置．

．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

（2012•和平区一模）如图分别表示甲、乙、丙三人由A地到B地的路线．
甲的路线为：A→C→B
乙的路线为：A→D→E→F→B，其中E为AB的中点
丙的路线为：A→I→J→K→B，其中J在AB上，且AJ＞JB
若符号「→」表示「直线前进」，判断三人行进路线长度的大小关系为（　　）

A．甲=乙=丙

B．甲＜乙＜丙

C．乙＜丙＜甲

D．丙＜乙＜甲

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

（2012•张家口一模）已知：如图1，⊙O与射线MN相切于点M，⊙O的半径为2，AC是⊙O的直径，A与M重合，△ABC是⊙O的内接三角形，且∠C=30°，
计算：弦AB=

2

2

，

AB

的长度

2

3

π

2

3

π

（结果保留π）
探究一：如图2，若⊙O和△ABC沿射线MN方向作无滑动的滚动，
（1）直接写出：点B第一次在射线MN上时，圆心O所走过的路线的长

2

3

π

2

3

π

点B第二次在射线MN上时，圆心O所走过的路线的长

14

3

π

14

3

π

（结果保留π）
（2）过点A、C分别作AD⊥MN于D，CE⊥MN于E，连接OD、OE，小明通过作图猜想：OD与OE相等，你认为小明的猜想正确吗？请说明你的理由
探究二：
如图3，将半径为R、圆心角为50°的扇形纸片AOB，在射线MN的方向作无滑动的滚动至扇形A′O′B′处，则顶点O经过的路线总长为

23

18

πR

23

18

πR

（用含R的代数式表示，结果保留π）．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

（2012•和平区一模）下列图形：

其中，可以看作是中心对称图形的有（　　）

A．1个

B．2个

C．3个

D．4个

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源：2010年河北省廊坊市文安县中考数学一模试卷（解析版） 题型：解答题

（2012•亳州一模）（1）如图1，已知△ABC，过点A画一条平分三角形面积的直线；
（2）如图2，已知l₁∥l₂，点E，F在l₁上，点G，H在l₂上，试说明△EGO与△FHO面积相等；
（3）如图3，点M在△ABC的边上，过点M画一条平分三角形面积的直线．

科目：czsx 来源：2009年浙江省温州市永嘉县中考数学二模试卷（解析版） 题型：选择题

科目：czsx 来源：2010年中考数学模拟试卷6（解析版） 题型：解答题

（2012•亳州一模）（1）如图1，已知△ABC，过点A画一条平分三角形面积的直线；
（2）如图2，已知l₁∥l₂，点E，F在l₁上，点G，H在l₂上，试说明△EGO与△FHO面积相等；
（3）如图3，点M在△ABC的边上，过点M画一条平分三角形面积的直线．

科目：czsx 来源： 题型：

（2012•闸北区一模）已知：如图，直线y=x-15与x轴、y轴分别相交于点A和点B．抛物线y=-

1

3

x2+bx+c经过A、B两点．
（1）求这个抛物线的解析式；
（2）若这抛物线的顶点为点D，与x轴的另一个交点为点C．对称轴与x轴交于点H，求△DAC的面积；
（3）若点E是线段AD的中点．CE与DH交于点G，点P在y轴的正半轴上，△POH是否能够与△CGH相似？如果能，请求出点P的坐标；如果不能，请说明理由．

科目：czsx 来源： 题型：

（2012•西城区一模）已知：如图1，矩形ABCD中，AB=6，BC=8，E、F、G、H分别是AB、BC、CD、DA四条边上的点（且不与各边顶点重合），设m=EF+FG+GH+HE，探索m的取值范围．
（1）如图2，当E、F、G、H分别是AB、BC、CD、DA四边中点时，m=

20

20

．
（2）为了解决这个问题，小贝同学采用轴对称的方法，如图3，将整个图形以CD为对称轴翻折，接着再连续翻折两次，
从而找到解决问题的途径，求得m的取值范围．①请在图3中补全小贝同学翻折后的图形；②m的取值范围是

20≤m＜28

20≤m＜28

．

科目：czsx 来源： 题型：

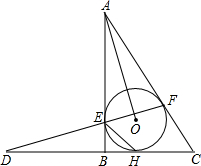（2012•宁波一模）已知：如图，Rt△ABC外切于⊙O，切点分别为E、F、H，∠ABC=90°，直线FE、CB交于D点，连接AO、HE，则下列结论：
①∠FEH=45°+∠FAO；②BD=AF；③AB²=AO•DF；④AE•CH=S_△ABC
其中正确的是（　　）

A．①②③④

B．①③④

C．②③④

D．①②③