如图,已知△ABC和△AEF中,AB=AC,AE=AF,∠CAB=∠EAF答案解析
科目:czsx
来源:
题型:
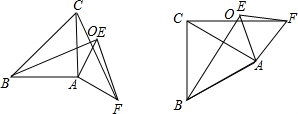
如图,已知△ABC和△AEF中,AB=AC,AE=AF,∠CAB=∠EAF,BE交FC于D点.
(1)当∠CAB=90゜时,求证:BE=CF,BE⊥CF;
(2)当∠CAB=60゜时,求∠BOC的度数;
(3)当∠CAB=α时(0゜<α<90゜),直接写出∠BOC的度数为
α
α
(用含及的式子表示).
查看答案和解析>>
科目:czsx
来源:
题型:解答题
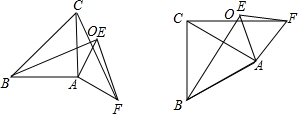
如图,已知△ABC和△AEF中,AB=AC,AE=AF,∠CAB=∠EAF,BE交FC于D点.
(1)当∠CAB=90゜时,求证:BE=CF,BE⊥CF;
(2)当∠CAB=60゜时,求∠BOC的度数;
(3)当∠CAB=α时(0゜<α<90゜),直接写出∠BOC的度数为______(用含及的式子表示).
查看答案和解析>>
科目:czsx
来源:
题型:

26、如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°;
(1)请说明∠EAB=∠FAC的理由;
(2)△ABC可以经过图形的变换得到△AEF,请你描述这个变换;
(3)求∠AMB的度数.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
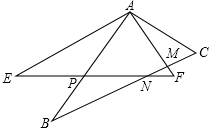 如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°;
如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°;
(1)请说明∠EAB=∠FAC的理由;
(2)△ABC可以经过图形的变换得到△AEF,请你描述这个变换;
(3)求∠AMB的度数.
查看答案和解析>>
科目:czsx
来源:
题型:
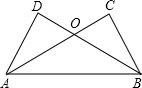
如图,已知△ABC和△BAD中,AC=DB,若不增加任何字母与辅助线,要证明△ABC≌△BAD;则还需要增加一个条件是
AD=BC
AD=BC
.
查看答案和解析>>
科目:czsx
来源:
题型:
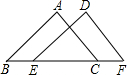
如图,已知△ABC和△DEF中,∠B=∠DEF,AB=DE,BE=CF.
①请说明∠A=∠D的理由;
②△ABC可以经过图形的变换得到△DEF,请你描述△ABC的变换过程.
查看答案和解析>>
科目:czsx
来源:
题型:

26、探究题.
如图,已知△ABC,∠BAC=90°,AB=AC,CD垂直于∠ABC角平分线BD于D,AC,BD交于E.AF为BC中线,交BE于G.
(1)求证:BE=2CD;
(2)CE和BG大小如何?不必证明.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,已知△ABC和△DEF中,∠B=∠DEF,AB=DE,BE=CF.
①请说明∠A=∠D的理由;
②△ABC可以经过图形的变换得到△DEF,请你描述△ABC的变换过程.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,已知△ABC和△DEF中,∠B=∠DEF,AB=DE,BE=CF.
如图,已知△ABC和△DEF中,∠B=∠DEF,AB=DE,BE=CF.
①请说明∠A=∠D的理由;
②△ABC可以经过图形的变换得到△DEF,请你描述△ABC的变换过程.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
探究题.
如图,已知△ABC,∠BAC=90°,AB=AC,CD垂直于∠ABC角平分线BD于D,AC,BD交于E.AF为BC 中线,交BE于G.
中线,交BE于G.
(1)求证:BE=2CD;
(2)CE和BG大小如何?不必证明.
查看答案和解析>>
科目:czsx
来源:浙江省期中题
题型:解答题
如图,已知△ABC和△DEF中,∠B=∠DEF,AB=DE,BE=CF。
①请说明∠A=∠D的理由;
②△ABC可以经过图形的变换得到△DEF,请你描述△ABC的变换过程。
查看答案和解析>>
科目:czsx
来源:
题型:
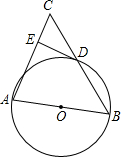
如图,已知△ABC是等腰三角形,AB=AC,AB是⊙O的直径,点D是BC的中点,且DE⊥AC,垂足为点E.
(1)求证:DE是⊙O的切线;
(2)若AB:BC=3:4,求∠C的正弦值.
查看答案和解析>>
科目:czsx
来源:
题型:
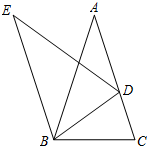
如图,已知△ABC为等腰三角形,AB=AC,△EBD通过旋转能与△ABC重合.
(1)旋转中心是
;
(2)如果旋转角恰好是△ABC底角度数的
,且AD=BD,那么旋转角的大小是
度;
(3)△BDC是
三角形.
查看答案和解析>>
科目:czsx
来源:
题型:
如图△ABC和△AEF中,AB=AC,AF=AE,∠BAC=∠EAF,FC,BE交于M,连接AM.
①如图1,若∠BAC=∠EAF=90°,则∠AME=
135°
135°
;
②如图2,若∠BAC=∠EAF=60°,则∠AME=
120°
120°
;
③如图3,若∠BAC=∠EAF=α,则∠AME=
,请证明你的结论.

查看答案和解析>>
科目:czsx
来源:2011年山东省临沂市中考数学模拟试卷(二)(解析版)
题型:解答题
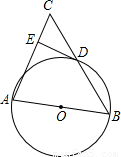
如图,已知△ABC是等腰三角形,AB=AC,AB是⊙O的直径,点D是BC的中点,且DE⊥AC,垂足为点E.
(1)求证:DE是⊙O的切线;
(2)若AB:BC=3:4,求∠C的正弦值.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,已知△ABC是等腰三角形,AB=AC,AB是⊙O的直径,点D是BC的中点,且DE⊥AC,垂足为点E.
如图,已知△ABC是等腰三角形,AB=AC,AB是⊙O的直径,点D是BC的中点,且DE⊥AC,垂足为点E.
(1)求证:DE是⊙O的切线;
(2)若AB:BC=3:4,求∠C的正弦值.
查看答案和解析>>
科目:czsx
来源:湖北省月考题
题型:解答题
如图△ABC和△AEF中,AB=AC,AF=AE,∠BAC=∠EAF,FC,BE交于M,连接AM。
①如图1,若∠BAC=∠EAF=90°,则∠AME= _________ ;
②如图2,若∠BAC=∠EAF=60°,则∠AME= _________ ;
③如图3,若∠BAC=∠EAF=α,则∠AME= _________ ,请证明你的结论。
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,已知△ABC为等腰三角形,AB=AC,△EBD通过旋转能与△ABC重合.
如图,已知△ABC为等腰三角形,AB=AC,△EBD通过旋转能与△ABC重合.
(1)旋转中心是______;
(2)如果旋转角恰好是△ABC底角度数的 ,且AD=BD,那么旋转角的大小是______度;
,且AD=BD,那么旋转角的大小是______度;
(3)△BDC是______三角形.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,已知△ABC为等腰三角形,AB=AC,△EBD通过旋转能与△ABC重合.
(1)旋转中心是______;
(2)如果旋转角恰好是△ABC底角度数的
,且AD=BD,那么旋转角的大小是______度;
(3)△BDC是______三角形.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
如图△ABC和△AEF中,AB=AC,AF=AE,∠BAC=∠EAF,FC,BE交于M,连接AM.
①如图1,若∠BAC=∠EAF=90°,则∠AME=________;
②如图2,若∠BAC=∠EAF=60°,则∠AME=________;
③如图3,若∠BAC=∠EAF=α,则∠AME=________,请证明你的结论.

查看答案和解析>>



 26、如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°;
26、如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°; 如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°;
如图,已知△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠EAB=25°,∠F=57°; 如图,已知△ABC和△DEF中,∠B=∠DEF,AB=DE,BE=CF.
如图,已知△ABC和△DEF中,∠B=∠DEF,AB=DE,BE=CF. 26、探究题.
26、探究题.
 如图,已知△ABC和△DEF中,∠B=∠DEF,AB=DE,BE=CF.
如图,已知△ABC和△DEF中,∠B=∠DEF,AB=DE,BE=CF. 中线,交BE于G.
中线,交BE于G.
 如图,已知△ABC是等腰三角形,AB=AC,AB是⊙O的直径,点D是BC的中点,且DE⊥AC,垂足为点E.
如图,已知△ABC是等腰三角形,AB=AC,AB是⊙O的直径,点D是BC的中点,且DE⊥AC,垂足为点E. 如图,已知△ABC为等腰三角形,AB=AC,△EBD通过旋转能与△ABC重合.
如图,已知△ABC为等腰三角形,AB=AC,△EBD通过旋转能与△ABC重合.

 如图,已知△ABC是等腰三角形,AB=AC,AB是⊙O的直径,点D是BC的中点,且DE⊥AC,垂足为点E.
如图,已知△ABC是等腰三角形,AB=AC,AB是⊙O的直径,点D是BC的中点,且DE⊥AC,垂足为点E.
 如图,已知△ABC为等腰三角形,AB=AC,△EBD通过旋转能与△ABC重合.
如图,已知△ABC为等腰三角形,AB=AC,△EBD通过旋转能与△ABC重合. ,且AD=BD,那么旋转角的大小是______度;
,且AD=BD,那么旋转角的大小是______度;
