科目:gzsx
来源:
题型:
已知△ABC内接于半径为1的圆O,且满足3
+4
+5
=
,则∠AOB=
,△ABC的面积S=
.
查看答案和解析>>
科目:gzsx
来源:2010年湖南省澧县一中、岳阳一中高三第三次联考数学试卷(理科)(解析版)
题型:解答题
已知△ABC内接于半径为1的圆O,且满足3

+4

+5
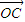
=
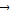
,则∠AOB=
,△ABC的面积S=
.
查看答案和解析>>
科目:gzsx
来源:湖南省岳澧二校2010届高三第三次联考(理)
题型:填空题
已知△ABC内接于半径为1的圆O,且满足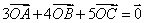 ,
,
则∠AOB=
,△ABC的面积S= .
查看答案和解析>>
科目:gzsx
来源:2012-2013学年江西南昌10所省高三第二次模拟冲刺理科数学试卷(六)(解析版)
题型:解答题
已知向量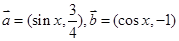 .
.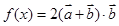
(1)求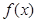 的增区间;
的增区间;
(2)已知△ ABC内接于半径为6的圆,内角A、B、C的对边分别
为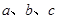 ,若
,若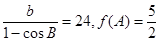 ,求边长
,求边长
查看答案和解析>>
科目:gzsx
来源:
题型:
已知正方形ABCD内接于半径为2、球心为O的球的截面小圆O',若小圆O'的半径为
,球面上五点S、A、B、C、D构成正四棱锥S-ABCD,且点S、O在平面ABCD异侧,则点S、C在该球面上的球面距离为
.
查看答案和解析>>
科目:gzsx
来源:2011年四川省成都七中高考数学模拟试卷2(理科)(解析版)
题型:解答题
已知正方形ABCD内接于半径为2、球心为O的球的截面小圆O',若小圆O'的半径为

,球面上五点S、A、B、C、D构成正四棱锥S-ABCD,且点S、O在平面ABCD异侧,则点S、C在该球面上的球面距离为
.
查看答案和解析>>
科目:gzsx
来源:导学大课堂必修二数学苏教版 苏教版
题型:044
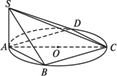
如下图,已知四边形ABCD内接于半径为R的⊙O,AC为⊙O的直径,点S为平面ABCD所在平面外一点,且SA⊥平面ABCD,∠DAC=∠ACB=∠SCA=30°,求二面角S-CB-A的正切值.
查看答案和解析>>
科目:gzsx
来源:
题型:044
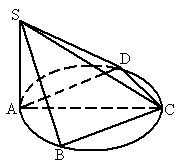
如图,已知四边形
ABCD内接于半径为R的⊙O,AC为⊙O的直径,点S为平面ABCD外的一点,且SA⊥平面ABCD,∠DAC=∠ACB=∠SCA=30°.求二面角S-CB-A的正切值的大小.
查看答案和解析>>
科目:gzsx
来源:数学教研室
题型:044
如图,已知四边形ABCD内接于半径为R的⊙O,AC为⊙O的直径,点S为平面ABCD外的一点,且SA⊥平面ABCD,∠DAC=∠ACB=∠SCA=30°.求二面角S-CB-A的正切值的大小.

查看答案和解析>>
科目:gzsx
来源:
题型:
如果△ABC内接于半径为R的圆,且
2R(sin2A-sin2C)=(a-b)sinB,求△ABC的面积的最大值.
查看答案和解析>>
科目:gzsx
来源:
题型:
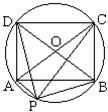
如图,矩形ABCD内接于半径为r的圆O,点P是圆周上任意一点,求证:PA
2+PB
2+PC
2+PD
2=8r
2.
查看答案和解析>>
科目:gzsx
来源:
题型:
如图,矩形ABCD内接于半径为r的圆O,点P是圆周上任意一点,求证:PA
2+PB
2+PC
2+PD
2=8r
2.

查看答案和解析>>
科目:gzsx
来源:广州市2008届高中教材变式题3:平面向量
题型:047
如图,矩形ABCD内接于半径为r的圆O,点P是圆周上任意一点,求证:PA2+PB2+PC2+PD2=8r2.

查看答案和解析>>
科目:gzsx
来源:
题型:解答题
如图,矩形ABCD内接于半径为r的圆O,点P是圆周上任意一点,求证:PA2+PB2+PC2+PD2=8r2.

查看答案和解析>>
科目:gzsx
来源:2008年高中数学平面向量试题
题型:047
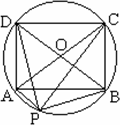
如图,矩形ABCD内接于半径为r的圆O,点P是圆周上任意一点,求证:PA2+PB2+PC2+PD2=8r2.
查看答案和解析>>
科目:gzsx
来源:
题型:
如图,矩形ABCD内接于半径为r的圆O,点P是圆周上任意一点,
求证:PA
2+PB
2+PC
2+PD
2=8r
2.
查看答案和解析>>
科目:gzsx
来源:
题型:
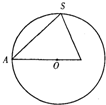
已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为
.
查看答案和解析>>
科目:gzsx
来源:2010年陕西省咸阳市礼泉一中高三5月最后一次预测数学试卷(解析版)
题型:解答题
已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为
.

查看答案和解析>>
科目:gzsx
来源:
题型:填空题
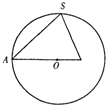 已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为________.
已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为________.
查看答案和解析>>

 +4
+4 +5
+5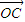 =
=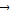 ,则∠AOB= ,△ABC的面积S= .
,则∠AOB= ,△ABC的面积S= . 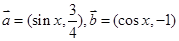 .
.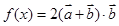
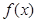 的增区间;
的增区间;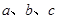 ,若
,若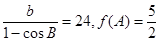 ,求边长
,求边长
 ,球面上五点S、A、B、C、D构成正四棱锥S-ABCD,且点S、O在平面ABCD异侧,则点S、C在该球面上的球面距离为 .
,球面上五点S、A、B、C、D构成正四棱锥S-ABCD,且点S、O在平面ABCD异侧,则点S、C在该球面上的球面距离为 . 



