
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| 3 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
科目:gzsx 来源:2010-2011学年山东省济宁市微山一中高一(下)期末数学试卷(解析版) 题型:解答题
 .函数f(x)=x2+x,数列{bn}的首项b1=
.函数f(x)=x2+x,数列{bn}的首项b1= .
. 求证:{cn}是等比数列并求{cn}通项公式;
求证:{cn}是等比数列并求{cn}通项公式;科目:gzsx 来源:河北省唐山一中2008-2009学年上学期高三期中考试(数学文) 题型:044
已知各项均为正数的数列{an}中,![]() ,前n项和
,前n项和![]() .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若![]() ,Tn为数列{bn}的前n项和,求证:Tn<1.
,Tn为数列{bn}的前n项和,求证:Tn<1.
科目:gzsx 来源:山东省微山一中2010-2011学年高一下学期期末考试数学试卷 题型:044
已知各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N*,有![]() .函数f(x)=x2+x,数列{bn}的首项
.函数f(x)=x2+x,数列{bn}的首项![]() .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令![]() 求证:{cn}是等比数列并求{cn}通项公式;
求证:{cn}是等比数列并求{cn}通项公式;
(Ⅲ)令dn=an·cn,(n为正整数),求数列{dn}的前n项和Tn.
科目:gzsx 来源:山东省模拟题 题型:解答题
 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.科目:gzsx 来源:0118 期中题 题型:解答题
科目:gzsx 来源:2011-2012学年山东省日照一中高三第七次阶段复习达标检测数学试卷(理科)(解析版) 题型:解答题
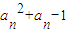 .函数f(x)=x2+x,数列{bn}的首项b1=
.函数f(x)=x2+x,数列{bn}的首项b1= .
. 求证:{cn}是等比数列并求{cn}通项公式;
求证:{cn}是等比数列并求{cn}通项公式;科目:gzsx 来源: 题型:解答题
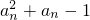 .函数f(x)=x2+x,数列{bn}的首项b1=
.函数f(x)=x2+x,数列{bn}的首项b1=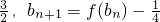 .
.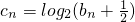 求证:{cn}是等比数列并求{cn}通项公式;
求证:{cn}是等比数列并求{cn}通项公式;科目:gzsx 来源:江苏省淮州中学2008届高三年级第二次调查测试数学试卷(理科) 题型:044
已知各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N*,有![]()
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
科目:gzsx 来源:江苏省淮州中学2008届高三年级第二次调查测试数学试卷理科 题型:044
已知各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N*,有2Sn=2p![]() +pan-p(p∈R)
+pan-p(p∈R)
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
科目:gzsx 来源: 题型:解答题
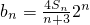 ,求数列bn的前n项和Tn.
,求数列bn的前n项和Tn.科目:gzsx 来源:河北省冀州中学2010-2011学年高一下学期期末考试数学理科试题(A卷) 题型:044
已知各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N*,有2Sn=2![]() +an-1.函数f(x)=x2+x,数列{bn}的首项
+an-1.函数f(x)=x2+x,数列{bn}的首项![]() .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令![]() 求证:{cn}是等比数列并求{cn}通项公式;
求证:{cn}是等比数列并求{cn}通项公式;
(Ⅲ)令dn=an·cn,(n为正整数),求数列{dn}的前n项和Tn.
科目:gzsx 来源:黑龙江省双鸭山市第一中学2011届高三上学期期中考试试题数学文综试题 题型:044
已知各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意的n∈N*,有2Sn=2pan2+pan-p(p∈R)
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记bn=![]() ·2n,求数列{bn}的前n项和Tn.
·2n,求数列{bn}的前n项和Tn.
科目:gzsx 来源:2007-2008学年江苏省无锡一中高三(上)期中数学试卷(解析版) 题型:解答题
科目:gzsx 来源:山东省日照一中2012届高三第七次阶段复习达标检测数学理科试题 题型:044
已知各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N*,有2Sn=![]() +an-1.函数f(x)=x2+x,数列{bn}的首项b1=
+an-1.函数f(x)=x2+x,数列{bn}的首项b1=![]() ,bn+1=f(b)-
,bn+1=f(b)-![]()
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令cn=log2(bn+![]() )求证:{cn}是等比数列并求{cn}通项公式;
)求证:{cn}是等比数列并求{cn}通项公式;
(Ⅲ)令dn=an·cn,(n为正整数),求数列{dn}的前n项和Tn.
科目:gzsx 来源: 题型:
A.100 B.1 000 C.10 000 D.10
科目:gzsx 来源:学习周报 数学 北师大课标高二版(必修5) 2009-2010学年 第4期 总第160期 北师大课标版(必修5) 题型:013
在已知各项均为正数的等比数列
{an}中,lg(a3a8a13)=6,则a1a15的值为10000
1000
100
10
科目:gzsx 来源:黑龙江省双鸭山一中2008-2009学年度高三上学期期中考试数学试卷(文) 题型:013
已知各项均为正数的等比数列{an}中,lg(a3·a8·a13)=6,则a1·a15的值为
A.100
B.1000
C.10000
D.10
科目:gzsx 来源: 题型:
|
| bn+1 |
| bn |