
科目:czsx 来源: 题型:
 抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C,
抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C,科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
科目:czsx 来源:2012届北京市西城区九年级下学期期末检测数学卷 题型:解答题
已知:抛物线 与x轴交于
与x轴交于
点A(x1,0)、B(x2,0),且x1<1<x2.
1.求A、B两点的坐标(用a表示);
2.设抛物线的顶点为C,求△ABC的面积;
3.若a是整数,P为线段AB上的一个动点(P点与A、B两点不重合),
在x轴上方作等边△APM和等边△BPN,记线段MN的中点为Q,求抛物线的
解析式及线段PQ的长的取值范围.
科目:czsx 来源:2013-2014学年江苏仪征大仪中九年级第一学期12月月考数学试卷(解析版) 题型:解答题
已知:抛物线 与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.
与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.
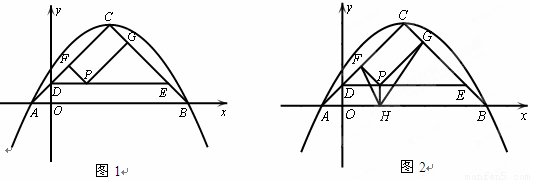
(1)求抛物线的解析式和点C的坐标;
(2)如图1,若AC交y轴于点D,过D点作DE∥AB交BC于E.点P为DE上一动点,PF⊥AC于F,PG⊥BC于G.设点P的横坐标为a,四边形CFPG的面积为y,求y与a的函数关系式和y的最大值;
(3)如图2,在条件(2)下,过P作PH⊥x轴于点H,连结FH、GH,是否存在点P,使得△PFH与△PHG相似?若存在,求出P点坐标;若不存在,说明理由.
科目:czsx 来源: 题型:
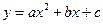 与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程
与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程 的两个根,且抛物线的对称轴是直线
的两个根,且抛物线的对称轴是直线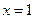 .
.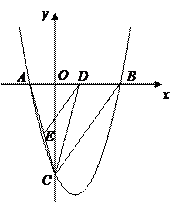
科目:czsx 来源: 题型:
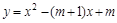 与x轴交于点A(
与x轴交于点A( ,0)、B(
,0)、B(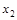 ,0)
,0)科目:czsx 来源:2010年安徽省芜湖市毕业学业考试模拟试卷数学卷 题型:解答题
(本小题满分12分)已知:抛物线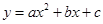 与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程
与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程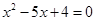 的两个根,且抛物线的对称轴是直线
的两个根,且抛物线的对称轴是直线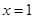 .
.

(1)求A、B、C三点的坐标;
(2)求此抛物线的解析式;
(3)若点D是线段AB上的一个动点(与点A、B不重合),过点D作DE∥BC交AC于点E,连结CD,设BD的长为m,△CDE的面积为S,求S与m的函数关系式,并写出自变量m的取值范围.S是否存在最大值?若存在,求出最大值并求此时D点坐标;若不存在,请说明理由.
科目:czsx 来源: 题型:
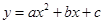 与x轴交于
与x轴交于 和
和 两点,与y轴交于
两点,与y轴交于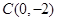 。
。
 为直角三角形?若存在,求出所有符合条件的点P的坐标,若不存在,请说明理由
为直角三角形?若存在,求出所有符合条件的点P的坐标,若不存在,请说明理由 科目:czsx 来源: 题型:
(本小题满分12分)已知:抛物线![]() 与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程
与x轴交于A、B两点,与y轴交于点C. 其中点A在x轴的负半轴上,点C在y轴的负半轴上,线段OA、OC的长(OA<OC)是方程![]() 的两个根,且抛物线的对称轴是直线
的两个根,且抛物线的对称轴是直线![]() .
.
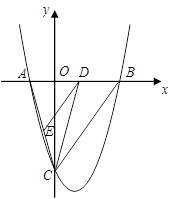
(1)求A、B、C三点的坐标;
(2)求此抛物线的解析式;
(3)若点D是线段AB上的一个动点(与点A、B不重合),过点D作DE∥BC交AC于点E,连结CD,设BD的长为m,△CDE的面积为S,求S与m的函数关系式,并写出自变量m的取值范围.S是否存在最大值?若存在,求出最大值并求此时D点坐标;若不存在,请说明理由.
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
. 已知:抛物线![]() 与x轴交于点A(
与x轴交于点A(![]() ,0)、B(
,0)、B(![]() ,0)
,0)
(A在B的左侧),与y轴交于点C.
1.(1)若m>1,△ABC的面积为6,求抛物线的解析式;
2.(2)点D在x轴下方,是(1)中的抛物线上的一个动点,且在该抛物线对称轴的左侧,作DE∥x轴与抛物线交于另一点E,作DF⊥x轴于F,作EG⊥x轴于点G,求矩形DEGF周长的最大值.
科目:czsx 来源: 题型:解答题
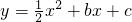 与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是
与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是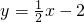 ,连接AC.
,连接AC.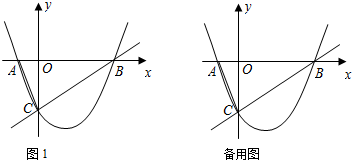
科目:czsx 来源:2011-2012学年北京市西城区九年级下学期期末检测数学卷 题型:解答题
已知:抛物线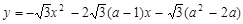 与x轴交于
与x轴交于
点A(x1,0)、B(x2,0),且x1<1<x2.
【小题1】求A、B两点的坐标(用a表示);
【小题2】设抛物线的顶点为C,求△ABC的面积;
【小题3】若a是整数,P为线段AB上的一个动点(P点与A、B两点不重合),
在x轴上方作等边△APM和等边△BPN,记线段MN的中点为Q,求抛物线的
解析式及线段PQ的长的取值范围.
科目:czsx 来源:2010-2011学年安徽省安庆市九年级(上)期中数学试卷(解析版) 题型:解答题
 与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是
与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是 ,连接AC.
,连接AC.
科目:czsx 来源: 题型:
已知:抛物线![]() 与x轴交于点
与x轴交于点![]() 、
、![]() ,与y轴交于点
,与y轴交于点![]() .直线
.直线![]() 与抛物线交于点
与抛物线交于点![]() 、
、![]() (
(![]() 在
在![]() 的左侧),与抛物线的对称轴交于点
的左侧),与抛物线的对称轴交于点![]() .
.
(1) 求抛物线的解析式;
(2) 当![]() 时,求
时,求![]() 的大小;
的大小;
(3) 若在直线![]() 下方的抛物线上存在点
下方的抛物线上存在点![]() ,使得
,使得![]() ,且满足条件的点
,且满足条件的点![]() 只有两个,则
只有两个,则![]() 的值为 .(第(3)问不要求写解答过程)
的值为 .(第(3)问不要求写解答过程)


备用图1 备用图2
科目:czsx 来源:2009-2010学年北京市师大附中九年级(上)期中数学试卷(解析版) 题型:解答题
科目:czsx 来源:2010-2011学年浙江省杭州市育才?锦绣中学九年级(上)月考数学试卷(10月份)(解析版) 题型:填空题
 与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是
与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是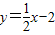 ,连接AC.则△ABC的形状 .
,连接AC.则△ABC的形状 . 科目:czsx 来源: 题型:解答题
科目:czsx 来源:2011年北京市石景山区中考数学二模试卷(解析版) 题型:解答题