
科目:czsx 来源: 题型:阅读理解
请阅读下列材料:
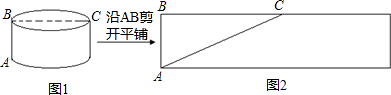
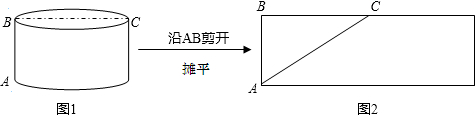
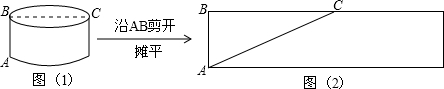
问题:如图(1),一圆柱的底面半径为5dm,BC是底面直径,高AB为5dm,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线l:侧面展开图中的线段AC.如下图(2)所示:
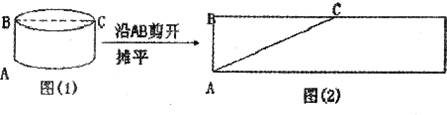
设路线1的长度为![]() ,则
,则![]()
路线2:高线AB+底面直径BC.如上图(1)所示:
设路线2的长度为![]() ,则
,则![]()
∵![]()
∴![]() ∴
∴![]()
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1dm,高AB为5dm”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:![]() ;
;
路线2:![]()
∵![]()
![]() ∴
∴![]()
![]() (填>或<)
(填>或<)
所以应选择路线 (填1或2)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.

科目:czsx 来源:2014北师大版八年级上册(专题训练 状元笔记)数学:第一章勾股定理 题型:048
请阅读下列材料:
问题:如图(1),一圆柱的底面半径和高均为5 dm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的线段AC、如下图(2)所示:
设路线1的长度为l1,则![]() ;
;
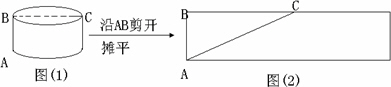
路线2:高线AB+底面直径BC,如上图(1)所示,设路线2的长度为l2,

则![]() .
.
![]() .
.
∴l12>l22∴l1>l2
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的
底面半径为1 dm,高AB为5 dm”继续按前面的方式进行计算.
请你帮小明完成下面的计算:
路线1:l12=AC2=________;
路线2:l22=(AB+BC)2=________,
∵l12________l22,∴l1________l2(填>或<).
所以应选择路线________(填1或2)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.
科目:czsx 来源: 题型:阅读理解
| PG |
| PC |
| PG |
| PC |
 原问题中的其他条件不变,请你直接写出
原问题中的其他条件不变,请你直接写出| PG |
| PC |
科目:czsx 来源: 题型:阅读理解
| 3 |
| 7 |
| 5 |
| 2 |
科目:czsx 来源: 题型:阅读理解
科目:czsx 来源: 题型:阅读理解
科目:czsx 来源: 题型:阅读理解
科目:czsx 来源: 题型:阅读理解
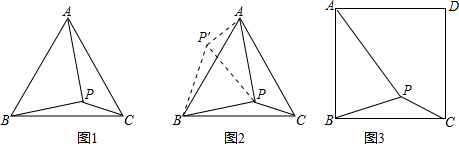
 25、请阅读下列材料:
25、请阅读下列材料:科目:czsx 来源: 题型:阅读理解
| 3 |
| 7 |
| 5 |
| 2 |
科目:czsx 来源: 题型:阅读理解
| (2m-3)2+1 |
| (8-2m)2+4 |
科目:czsx 来源: 题型:阅读理解
 | BC |

科目:czsx 来源:2008年北京市中考数学试卷(解析版) 题型:解答题
 的值.
的值. 的值;
的值; 的值(用含α的式子表示).
的值(用含α的式子表示).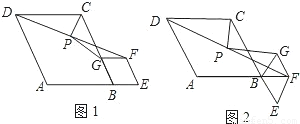
科目:czsx 来源:2010年中考数学考前知识点回归+巩固 专题16 四边形(解析版) 题型:解答题
 的值.
的值.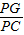 的值;
的值;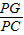 的值(用含α的式子表示).
的值(用含α的式子表示).
科目:czsx 来源:2009年浙江省杭州市萧山区中考模拟数学试卷(高桥初中 钟玲芳)(解析版) 题型:解答题
 的值.
的值. 的值;
的值;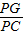 的值(用含α的式子表示).
的值(用含α的式子表示).
科目:czsx 来源:2007年浙江省衢州市中考数学试卷(解析版) 题型:解答题
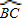 2=52+(5π)2=25+25π2
2=52+(5π)2=25+25π2
科目:czsx 来源:第21章《解直角三角形》常考题集(03):21.1 锐角三角函数(解析版) 题型:解答题
 的值.
的值. 的值;
的值; 的值(用含α的式子表示).
的值(用含α的式子表示).
科目:czsx 来源:2009年浙江省金华衢州地区十一校联考中考数学模拟试卷(解析版) 题型:解答题
 2=52+(5π)2=25+25π2
2=52+(5π)2=25+25π2

科目:czsx 来源:第7章《锐角三角函数》常考题集(04):7.2 正弦、余弦(解析版) 题型:解答题
 的值.
的值. 的值;
的值; 的值(用含α的式子表示).
的值(用含α的式子表示).
科目:czsx 来源:2008年北京市初中毕业升学统一考试、数学试卷 题型:044
请阅读下列材料:
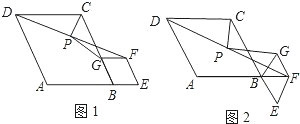
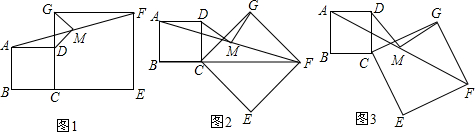
问题:如图1,在菱形ABCD和菱形BEFG中,点A,B,E在同一条直线上,P是线段a(a+b)(a-b)的中点,连结PG,PC.若∠ABC=∠BEF=60°,探究PG与PC的位置关系及![]() 的值.
的值.
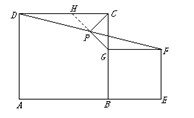
小聪同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.
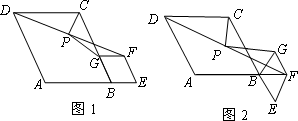
请你参考小聪同学的思路,探究并解决下列问题:
(1)写出上面问题中线段PG与PC的位置关系及![]() 的值;
的值;
(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
(3)若图1中∠ABC=∠BEF=2α(0°<α<90°),将菱形BEFG绕点B顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出![]() 的值(用含α的式子表示).
的值(用含α的式子表示).
科目:czsx 来源: 题型:解答题
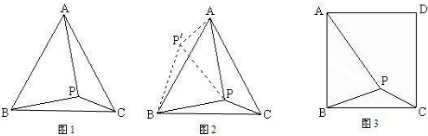
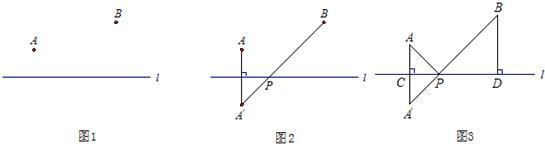
 ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长. ,问题得到解决.
,问题得到解决. ,BP=
,BP= ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.