
科目:czsx 来源: 题型:
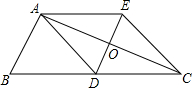 (2012•建宁县质检)如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.
(2012•建宁县质检)如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.科目:czsx 来源: 题型:
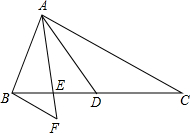 (2012•松江区一模)已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.
(2012•松江区一模)已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.| 3 |
科目:czsx 来源: 题型:
 3、如图,在△ABC中,AD是高,△ABC的外接圆直径AE交BC边于点G,有下列四个结论:①AD2=BD•CD;②BE2=EG•AE;③AE•AD=AB•AC;④AG•EG=BG•CG.其中正确结论的个数是( )
3、如图,在△ABC中,AD是高,△ABC的外接圆直径AE交BC边于点G,有下列四个结论:①AD2=BD•CD;②BE2=EG•AE;③AE•AD=AB•AC;④AG•EG=BG•CG.其中正确结论的个数是( )科目:czsx 来源: 题型:
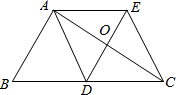 22、如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
22、如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.科目:czsx 来源: 题型:
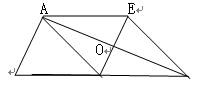
 (2013•莒南县一模)如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC
(2013•莒南县一模)如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC科目:czsx 来源: 题型:
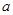 ,求菱形ADCE的周长.(5分)
,求菱形ADCE的周长.(5分) 科目:czsx 来源: 题型:
如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.
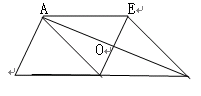
1.求证:AD=EC;(4分)
2.当∠BAC=90º时,求证:四边形ADCE是菱形;(3分)
3.在(2)的条件下,若AB=AO,且OD=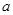 ,求菱形ADCE的周长.(5分)
,求菱形ADCE的周长.(5分)
科目:czsx 来源: 题型:

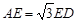 ,求证:
,求证: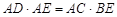 .
. 科目:czsx 来源:2011-2012学年江苏省扬州市邗沟中学九年级第一学期期末考试数学卷 题型:解答题
(本题满分8分)如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、点E,连接EC.
【小题1】(1)求证:AD=EC;
【小题2】(2)当∠BAC=90°时,求证:四边形ADCE是菱形;
科目:czsx 来源:2011-2012学年上海市松江区中考一模数学卷 题型:解答题
(本题满分12分,其中第(1)小题5分,第(2)小题7分)
已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.
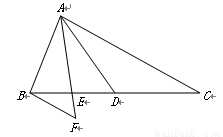
1.(1)求证:AC=3BF;
2.(2)如果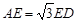 ,求证:
,求证: .
.
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
(本题满分12分,其中第(1)小题5分,第(2)小题7分)
已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.

1.(1)求证:AC=3BF;
2.(2)如果![]() ,求证:
,求证:![]() .
.
科目:czsx 来源:2012-2013学年山东省潍坊市九年级学业水平模拟考试(二模)数学试卷.(解析版) 题型:解答题
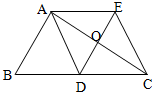
如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.

(1)求证:AD=EC;
(2)当∠BAC= 时,求证:四边形ADCE是菱形.
时,求证:四边形ADCE是菱形.
科目:czsx 来源:2012届福建建宁九年级学业质量检测考试数学试卷(带解析) 题型:解答题
如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.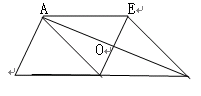
【小题1】求证:AD=EC;(4分)
【小题2】当∠BAC=90º时,求证:四边形ADCE是菱形;(3分)
【小题3】在(2)的条件下,若AB=AO,且OD=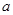 ,求菱形ADCE的周长.(5分)
,求菱形ADCE的周长.(5分)
科目:czsx 来源:2011-2012学年福建建宁九年级学业质量检测考试数学试卷(解析版) 题型:解答题
如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.

1.求证:AD=EC;(4分)
2.当∠BAC=90º时,求证:四边形ADCE是菱形;(3分)
3.在(2)的条件下,若AB=AO,且OD= ,求菱形ADCE的周长.(5分)
,求菱形ADCE的周长.(5分)
科目:czsx 来源: 题型:

科目:czsx 来源:2011年初中毕业升学考试(山东烟台卷)数学 题型:解答题
(2011•衢州)如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.
科目:czsx 来源:2013届山东省潍坊市九年级学业水平模拟考试(二模)数学试卷.(带解析) 题型:解答题
如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC= 时,求证:四边形ADCE是菱形.
时,求证:四边形ADCE是菱形.
科目:czsx 来源:2011-2012学年上海市松江区中考一模数学卷 题型:解答题
(本题满分12分,其中第(1)小题5分,第(2)小题7分)
已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.
【小题1】(1)求证:AC=3BF;
【小题2】(2)如果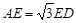 ,求证:
,求证: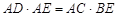 .
.
科目:czsx 来源:2011-2012年江苏省扬州市九年级第一学期期末考试数学卷 题型:解答题
(本题满分8分)如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、点E,连接EC.
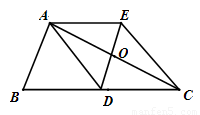
1.(1)求证:AD=EC;
2.(2)当∠BAC=90°时,求证:四边形ADCE是菱形;