精英家教网 >
试题搜索列表 >如果求1+3+3的2次幂+3的3次幂+····+3的20次幂的值,可令S=1+3+3的2次幂+3的3次幂+···+3的20次幂,1。将1式两边同乘以3,得————2.有2式减去1式,得S=2分之1(3的21次幂-1)
如果求1+3+3的2次幂+3的3次幂+····+3的20次幂的值,可令S=1+3+3的2次幂+3的3次幂+···+3的20次幂,1。将1式两边同乘以3,得————2.有2式减去1式,得S=2分之1(3的21次幂-1)答案解析
科目:czsx
来源:
题型:
二次函数
y=x2-x+6的图象与x轴从左到右两个交点依次为A、B,与y轴交于点C.
(1)求A、B、C三点的坐标;
(2)如果P(x,y)是线段BC之间的动点,O为坐标原点,试求△POA的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,是否存在这样的点P,使得PO=PA?若存在,求出点P的坐标;若不存在请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
“人间四月天,花城看杜鹃”,为了迎接八方宾朋的到来,黄冈某地市政府把市区主要路段路灯更换为太阳能路灯;已知太阳能路灯售价为5000元/个,目前两个商家有此产品;甲商家用如下方法促销:若购买路灯不超过100个,按原价付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但太阳能路灯的售价不得低于3500元/个;乙店一律按原价的80%销售;现购买太阳能路灯x个,如果全部在甲商家购买,则所需金额为y1元;如果全部在乙商家购买,则所需金额为y2元;
(1)求y1与x之间的函数关系式;
(2)写y2与x之间的函数关系式;
(3)若市政府投资140万元,最多能购买多少个太阳能路灯?
查看答案和解析>>
科目:czsx
来源:
题型:
已知A=5x2-mx+n,B=3y2-2x+1.如果A-B的结果中不含一次项和常数项,求m2+n2-2mn的值.
查看答案和解析>>
科目:czsx
来源:
题型:

(2012•娄底)已知二次函数y=x
2-(m
2-2)x-2m的图象与x轴交于点A(x
1,0)和点B(x
2,0),x
1<x
2,与y轴交于点C,且满足
+=.
(1)求这个二次函数的解析式;
(2)探究:在直线y=x+3上是否存在一点P,使四边形PACB为平行四边形?如果有,求出点P的坐标;如果没有,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
一次数学兴趣活动,小明提出这样三个问题,请你解决:
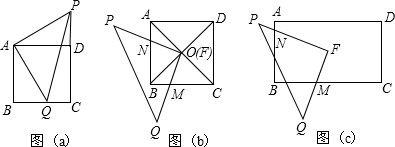
(1)把正方形ABCD与等腰Rt△PAQ如图(a)所示重叠在一起,其中∠PAQ=90°,点Q在边BC上,连接PD,求证:△ADP≌△ABQ.
(2)如图(b),O为正方形ABCD对角线的交点,将一直角三角板FPQ的直角顶点F与点O重合,转动三角板使两直角边始终与BC、AB相交于点M、N,求证:OM=ON.
(3)如图(c),将(2)的“正方形”改为“矩形”,其它条件不变,如果AB=4,AD=6,FM=x,FN=y,试求y与x之间的关系式.
查看答案和解析>>
科目:czsx
来源:
题型:
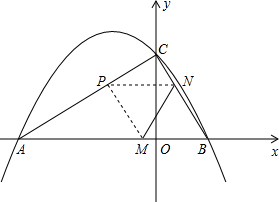
如图,二次函数y=ax
2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴相交于点C.连接AC,BC,A(-3,0),C(0,
),且当x=-4和x=2时二次函数的函数值y相等.
(1)求抛物线的解析式;
(2)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动.
①当运动时间为t秒时,连接MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,求t的值及点P的坐标;
②抛物线的对称轴上是否存在点Q,使得以B、N、Q为顶点的三角形与△A0C相似?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
③当运动时间为t秒时,连接MN,将△BMN沿MN翻折,得到△PMN.并记△PMN与△AOC的重叠部分的面积为S.求S与t的函数关系式.
查看答案和解析>>
科目:czsx
来源:
题型:
在口袋中装有23个号码球,分别标有1~23共23个数字,各小球除了号码不同外完全相同,现在从中随意取出两个小球,求:
(1)第一次取出的小球号码大于9的概率;
(2)第一次取出的小球号码小于30的概率;
(3)如果第一次取出的小球是3,不放回,求第二次取出的小球号码大于9的概率;
(4)如果第一次取出的小球是6,也不放回,再求第二次取出的小球号码是偶数的概率.
查看答案和解析>>
科目:czsx
来源:
题型:
如果x2m-3y4+xym+1是五次多项式,求m的值.
查看答案和解析>>
科目:czsx
来源:
题型:
如果关于x,y的二元一次方程组
的解是正整数,求整数p的值.
查看答案和解析>>
科目:czsx
来源:
题型:
在预防流感期间某住宅小区的活动室坚持天天消毒,下图是某次消毒时活动室内空气中消毒液浓度y(单位:毫克/立方米)随时间 x(单位:分钟)的变化情况图.从开始喷药

到喷药结束的10分钟内(包括第十分钟),y是x的二次函数;喷药结束后(从第十分钟开始),y是x的反比例函数.
(1)如果点A是图中二次函数的顶点,求二次函数和反比例函数的解析式 (要写出自变量取值范围);
(2)已知空气中消毒液浓度y不少于15毫克/立方米且持续时间不少于8分钟才能有效消毒,通过计算,请你回答这次消毒是否有效?
查看答案和解析>>
科目:czsx
来源:
题型:

(2012•日照)如图,二次函数y=x
2+bx+c的图象与x轴交于A、B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).
(1)求抛物线的解析式和直线BD解析式;
(2)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD,交抛物线于点F,是否存在实数a使四边形BDFE是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
电脑中有一种游戏-“蜘蛛”,开始游戏前有500分的基本分,游戏规则如下:
①每操作一次减x分
②每完成一列加y分
小明在一次玩这种“蜘蛛”游戏时,随手用表格记录了2个时段电脑显示
|
第一时段 |
第二时段 |
| 完成列数 |
2 |
5 |
| 分数 |
634 |
898 |
| 操作列数 |
66 |
102 |
(1)通过列方程组,求x、y的值?
(2)如果小明最终此游戏(即完成8列),分数是1182,问他一共操作多少次?
查看答案和解析>>
科目:czsx
来源:
题型:
已知:抛物线y=x2+bx+c的对称轴是x=2,且经过点A(1,0),且与x轴的另一个交点为B,与y轴交于点C,
(1)确定此二次函数的解析式及顶点D的坐标;
(2)将直线CD沿y轴向下平移3个单位长度,求平移后直线m的解析式.
(3)在直线m上是否存在一点E,使得以点E、A、B、C为顶点的四边形是梯形,如果存在,求出满足条件的E点的坐标,如果不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
有两个可以自由转动的均匀转盘A、B,分别被分成4等份、3等份,并在每份内均
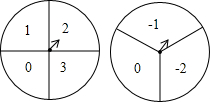
标有数字,如图所示.王扬和刘菲同学用这两个转盘做游戏,游戏规则如下:
①分别转动转盘A与B;
②两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止).
③如果和为0,王扬获胜;否则刘非获胜.
(1)用列表法(或树状图)求王扬获胜的概率;
(2)你认为这个游戏对双方公平吗?请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
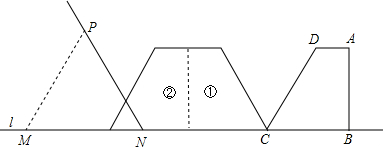
已知:如图,在直角梯形ABCD中,AD∥BC,BC=5,CD=6,∠DCB=60°,∠ABC=90°.等边三角形MPN(N为不动点)的边长为a,边MN和直角梯形ABCD的底边BC都在直线l上,NC=8.将直角梯形ABCD向左翻折180°,翻折一次得到图形①,翻折二次得到图形②,如此翻折下去.
(1)求直角梯形ABCD的面积;
(2)将直角梯形ABCD向左翻折二次,如果此时等边三角形的边长a≥2,请直接写出这时两图形重叠部分的面积是多少?
(3)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积,请直接写出这时等边三角形的边长a至少应为多少?
查看答案和解析>>
科目:czsx
来源:
题型:
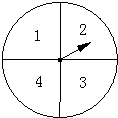
有一个可自由转动的转盘,被分成了4个相同的扇形,分别标有数1,2,3,4(如图所示),另有一个不透明的口袋装有分别标有数0,1,3的三个小球(除数不同外,其余都相同),小亮转动一次转盘,停止后指针指向某一扇形,扇形内的数是小亮的幸运数,小红任意摸出一个小球,小球上的数是小红的吉祥数,然后计算这两个数的积.
(1)请你用画树状图或列表的方法,求这两个数的积为0的概率;
(2)小亮与小红做游戏,规则是:若这两个数的积为奇数,小亮赢;否则,小红赢.你认为该游戏公平吗?为什么?如果不公平,请你修改该游戏规则,使游戏公平.
查看答案和解析>>
科目:czsx
来源:
题型:
因国务院有关房地产的新政策出台后,某楼盘平均成交价由今年2月份的6000元/m
2下降到4月份的5400元/m
2(假设每月降价一次,且降幅相同).
(1)求平均每次下降的百分率;(参考数据:
≈0.95)
(2)如果房价继续回落,按此降价的百分率,你预测到6月份该楼盘成交均价是否会跌破4800元/m
2?请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

为了给市民提供一个休闲健身的场所,市政府决定将一块矩形(如图)空地规划成休闲广场,初步规划AB为1200米,BC长为400米,后经测量发现,如果AB长每减少30米,则BC长就可增加20米,为了合理的利用土地,AB长又不能小于600米,设AB边的长为x米.矩形休闲广场的占地面积为S平方米.
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围)
(2)当x为何值时,S有最大值?并求出最大值.
(参考公式:二次函数y=ax
2+bx+c(a≠0),当x=-
时,y
最大(小)值=
)
查看答案和解析>>
科目:czsx
来源:
题型:
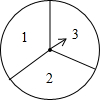
(2013•宿城区一模)如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.
(1)转动转盘两次,用画树状图或列表的方法求两次指针所指区域数字不同的概率;
(2)在第(1)题中,两次转到的区域的数字作为两条线段的长度,如果第三条线段的长度为5,求这三条线段能构成三角形的概率.
查看答案和解析>>
科目:czsx
来源:
题型:
已知y=m
2+m+4,若m为整数,在使得y为完全平方数的所有m的值中,设m的最大值为a,最小值为b,次小值为c.(注:一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数.)
(1)求a、b、c的值;
(2)对a、b、c进行如下操作:任取两个求其和再除以
,同时求其差再除以
,剩下的另一个数不变,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,所得三个数的平方和等于2008证明你的结论.
查看答案和解析>>

 (2012•娄底)已知二次函数y=x2-(m2-2)x-2m的图象与x轴交于点A(x1,0)和点B(x2,0),x1<x2,与y轴交于点C,且满足
(2012•娄底)已知二次函数y=x2-(m2-2)x-2m的图象与x轴交于点A(x1,0)和点B(x2,0),x1<x2,与y轴交于点C,且满足
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴相交于点C.连接AC,BC,A(-3,0),C(0,
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴相交于点C.连接AC,BC,A(-3,0),C(0, 到喷药结束的10分钟内(包括第十分钟),y是x的二次函数;喷药结束后(从第十分钟开始),y是x的反比例函数.
到喷药结束的10分钟内(包括第十分钟),y是x的二次函数;喷药结束后(从第十分钟开始),y是x的反比例函数. (2012•日照)如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).
(2012•日照)如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3). 标有数字,如图所示.王扬和刘菲同学用这两个转盘做游戏,游戏规则如下:
标有数字,如图所示.王扬和刘菲同学用这两个转盘做游戏,游戏规则如下:
 有一个可自由转动的转盘,被分成了4个相同的扇形,分别标有数1,2,3,4(如图所示),另有一个不透明的口袋装有分别标有数0,1,3的三个小球(除数不同外,其余都相同),小亮转动一次转盘,停止后指针指向某一扇形,扇形内的数是小亮的幸运数,小红任意摸出一个小球,小球上的数是小红的吉祥数,然后计算这两个数的积.
有一个可自由转动的转盘,被分成了4个相同的扇形,分别标有数1,2,3,4(如图所示),另有一个不透明的口袋装有分别标有数0,1,3的三个小球(除数不同外,其余都相同),小亮转动一次转盘,停止后指针指向某一扇形,扇形内的数是小亮的幸运数,小红任意摸出一个小球,小球上的数是小红的吉祥数,然后计算这两个数的积. 为了给市民提供一个休闲健身的场所,市政府决定将一块矩形(如图)空地规划成休闲广场,初步规划AB为1200米,BC长为400米,后经测量发现,如果AB长每减少30米,则BC长就可增加20米,为了合理的利用土地,AB长又不能小于600米,设AB边的长为x米.矩形休闲广场的占地面积为S平方米.
为了给市民提供一个休闲健身的场所,市政府决定将一块矩形(如图)空地规划成休闲广场,初步规划AB为1200米,BC长为400米,后经测量发现,如果AB长每减少30米,则BC长就可增加20米,为了合理的利用土地,AB长又不能小于600米,设AB边的长为x米.矩形休闲广场的占地面积为S平方米. (2013•宿城区一模)如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.
(2013•宿城区一模)如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.