
科目:gzsx 来源: 题型:
| A、将△ABD沿BD翻转到任意位置时,直线AC与直线BD都垂直 | ||||
| B、当平面ABD垂直于平面BCD时,此时∠ACD=60° | ||||
C、沿BD翻转到某个位置时,使得三棱锥A-BCD体积最大值是
| ||||
| D、沿BD翻转到任意位置时,三直线“AB与CD”,“AD与BC”,“AC与BD”均不垂直 |
科目:gzsx 来源: 题型:
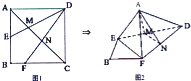 (2012•泉州模拟)如图l,在正方形ABCD中,AB=2,E是AB边的中点,F是BC边上的一点,对角线AC分别交DE、DF于M、N两点.将ADAE,CDCF折起,使A、C重合于A点,构成如图2所示的几何体.
(2012•泉州模拟)如图l,在正方形ABCD中,AB=2,E是AB边的中点,F是BC边上的一点,对角线AC分别交DE、DF于M、N两点.将ADAE,CDCF折起,使A、C重合于A点,构成如图2所示的几何体.科目:gzsx 来源: 题型:
A.![]() a+
a+![]() b B.
b B.![]() a+
a+![]() b C.
b C.![]() a+
a+![]() b D.
b D.![]() a+
a+![]() b
b
科目:gzsx 来源:福建省泉州市普通中学2012届高中毕业班质量检查数学文科试题 题型:044
如图1,在正方形ABCD中,AB=2,E是AB边的中点,F是BC边上的一点,对角线AC分别交DE、DF于M、N两点.将△DAE,△DCF折起,使A、C重合于![]() 点,构成如图2所示的几何体.
点,构成如图2所示的几何体.
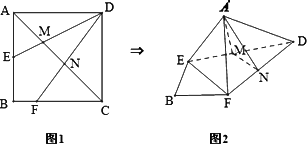
(Ⅰ)求证:![]() D⊥面
D⊥面![]() EF;
EF;
(Ⅱ)试探究:在图1中,F在什么位置时,能使折起后的几何体中EF∥平面AMN,并给出证明.
科目:gzsx 来源:2011-2012年河南省豫东六校联谊高三第一次联考数学试卷(文科)(解析版) 题型:解答题

科目:gzsx 来源:2012年福建省泉州市高三3月质量检查数学试卷(文科)(解析版) 题型:解答题

科目:gzsx 来源:河南省模拟题 题型:解答题
科目:gzsx 来源: 题型:

(1)求证:![]() 是定值.
是定值.
(2)已知P是SC的中点,且SO=3,问在棱SA上是否存在一点Q,使异面直线OP与BQ所成的角为90°?若存在,请给出证明,并求出AQ的长;若不存在,请说明理由.
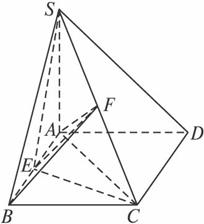
(文)如图,在四棱锥S—ABCD中,底面ABCD是正方形,SA⊥平面ABCD,且SA=AB,点E为AB的中点,点F为SC的中点.

(1)求证:EF⊥CD;
(2)求证:平面SCD⊥平面SCE.
科目:gzsx 来源: 题型:

(1)求证:![]() 是定值.
是定值.
(2)已知P是SC的中点,且SO=3,问在棱SA上是否存在一点Q,使异面直线OP与BQ所成的角为90°?若存在,请给出证明,并求出AQ的长;若不存在,请说明理由.
(文)如图,在四棱锥S—ABCD中,底面ABCD是正方形,SA⊥平面ABCD,且SA=AB,点E为AB的中点,点F为SC的中点.
(1)求证:EF⊥CD;
(2)求证:平面SCD⊥平面SCE.
科目:gzsx 来源: 题型:解答题
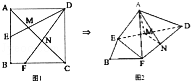
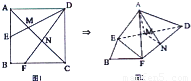
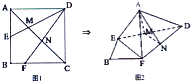 如图l,在正方形ABCD中,AB=2,E是AB边的中点,F是BC边上的一点,对角线AC分别交DE、DF于M、N两点.将ADAE,CDCF折起,使A、C重合于A点,构成如图2所示的几何体.
如图l,在正方形ABCD中,AB=2,E是AB边的中点,F是BC边上的一点,对角线AC分别交DE、DF于M、N两点.将ADAE,CDCF折起,使A、C重合于A点,构成如图2所示的几何体.科目:gzsx 来源:2011-2012学年河南省中原六校高三第一次联考数学试卷(文科)(解析版) 题型:解答题
科目:gzsx 来源:云南省玉溪一中11-12学年高二上学期期中考试数学试题 题型:选择题
在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F,若 =a,
=a, =b,则
=b,则 等于( )
等于( )
A.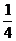 a+
a+ b
B.
b
B.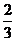 a+
a+ b
C.
b
C. a+
a+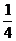 b D.
b D. a+
a+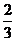 b
b
科目:gzsx 来源: 题型:单选题
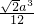
科目:gzsx 来源: 题型:
 (2010•昆明模拟)如图,在正方形ABCD中,E、F分别是BC、CD的中点,AC∩EF=G.现在沿AE、EF、FA把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,则在四面体P-AEF中必有( )
(2010•昆明模拟)如图,在正方形ABCD中,E、F分别是BC、CD的中点,AC∩EF=G.现在沿AE、EF、FA把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,则在四面体P-AEF中必有( )科目:gzsx 来源: 题型:
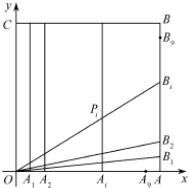 (2013•福建)如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点
(2013•福建)如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点| P | i |
| P | i |
科目:gzsx 来源: 题型:
 在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,顶点S在底面内的射影O在正方形ABCD的内部(不在边上),且SO=λa,λ为常数,设侧面SAB,SBC,SCD,SDA与底面ABCD所成的二面角依次为α1,α2,α3,α4,则下列各式为常数的是
在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,顶点S在底面内的射影O在正方形ABCD的内部(不在边上),且SO=λa,λ为常数,设侧面SAB,SBC,SCD,SDA与底面ABCD所成的二面角依次为α1,α2,α3,α4,则下列各式为常数的是科目:gzsx 来源: 题型:
 如图,面积为S的正方形ABCD中有一个不规则的图形M,可按下面方法估计M的面积:在正方形ABCD中随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为
如图,面积为S的正方形ABCD中有一个不规则的图形M,可按下面方法估计M的面积:在正方形ABCD中随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为| m |
| n |
| k |
 |
| t=0 |
| C | t 10000 |
