已知正方形棱长为a，P是A1D1上的定点，Q是C1D1上的动点答案解析
科目：gzsx
来源：
题型：
已知正方形ABCD—A
1B
1C
1D
1的棱长为a，P在AB上，且PB=2PA.
(1)求二面角A1PCA的余弦值；
(2)求B1到面A1PC的距离.
查看答案和解析>>
科目：gzsx
来源：
题型：
已知正方形ABCD—A
1B
1C
1D
1的棱长为a，P在AB上，且PB=2PA.
(1)求二面角A1PCA的余弦值；
(2)求B1到面A1PC的距离.
查看答案和解析>>
科目：gzsx
来源：
题型：
已知一棱长为a的正方体,则与其中一条棱所在直线异面,并且距离为a的棱共有( )
A.4条 B.5条 C.6条 D.7条
查看答案和解析>>
科目：gzsx
来源：
题型：
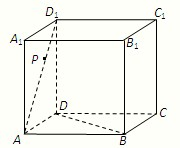
正方体ABCD-A
1B
1C
1D
1的棱长为a，P是面对角线AD
1上的动点，点P到BD的距离记为d，求d的最小值，并指出d取最小值时点P的位置．
查看答案和解析>>
科目：gzsx
来源：
题型：
设等边△ABC的边长为a，P是△ABC内任意一点，且P到三边AB、BC、CA的距离分别为d
1、d
2、d
3，则有d
1+d
2+d
3为定值
a；由以上平面图形的特性类比到空间图形：设正四面体ABCD的棱长为a，P是正四面体ABCD内任意一点，且P到平面ABC、平面ABD、平面ACD、平面BCD的距离分别为h
1、h
2、h
3、h
4，则有h
1+h
2+h
3+h
4为定值
．
查看答案和解析>>
科目：gzsx
来源：
题型：
设等边△ABC的边长为a，P是△ABC内的任意一点，且P到三边AB，BC，CA的距离分别为d
1，d
2，d
3，则有d
1+d
2+d
3为定值
a；由以上平面图形的特性类比空间图形：设正四面体ABCD的棱长为a，P是正四面体ABCD内的任意一点，且P到四个面ABC、ABD、ACD、BCD的距离分别为d
1，d
2，d
3，d
4，则有d
1+d
2+d
3+d
4为定值
．
查看答案和解析>>
科目：gzsx
来源：
题型：
如图所示，正方体
ABCD—
EFGH的棱长为
a,点
P在
AC上，
Q在
BG上，
AP=
BQ=
a.
（1）求直线PQ与平面ABCD所成角的正切值；
（2）求证：PQ⊥AD.
查看答案和解析>>
科目：gzsx
来源：不详
题型：填空题
设等边△ABC的边长为a，P是△ABC内的任意一点，且P到三边AB，BC，CA的距离分别为d
1，d
2，d
3，则有d
1+d
2+d
3为定值
a；由以上平面图形的特性类比空间图形：设正四面体ABCD的棱长为a，P是正四面体ABCD内的任意一点，且P到四个面ABC、ABD、ACD、BCD的距离分别为d
1，d
2，d
3，d
4，则有d
1+d
2+d
3+d
4为定值______．
查看答案和解析>>
科目：gzsx
来源：
题型：解答题
正方体ABCD-A1B1C1D1的棱长为a，P是面对角线AD1上的动点，点P到BD的距离记为d，求d的最小值，并指出d取最小值时点P的位置．
查看答案和解析>>
科目：gzsx
来源：
题型：044
如图，正方体ABCD－A1B1C1D1的棱长为a，P是B1C1的中点，A1C1与PD1交于M，B1C与PB交于N，求证：MN⊥A1C1，MN⊥B1C，并求MN的长
查看答案和解析>>
科目：gzsx
来源：
题型：022
在正方体
ABCD——
中，棱长为a，P是面ABCD的中心，Q是
的中点，则|PQ|=_________________．
查看答案和解析>>
科目：gzsx
来源：数学教研室
题型：044
如图，正方体ABCD－A1B1C1D1的棱长为a，P是B1C1的中点，A1C1与PD1交于M，B1C与PB交于N，求证：MN⊥A1C1，MN⊥B1C，并求MN的长
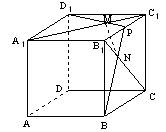
查看答案和解析>>
科目：gzsx
来源：数学教研室
题型：022
在正方体ABCD——
中，棱长为a，P是面ABCD的中心，Q是
的中点，则|PQ|=_________________．
查看答案和解析>>
科目：gzsx
来源：2010年江苏省徐州一中高三数学提优练习（11）（解析版）
题型：解答题
正方体ABCD-A
1B
1C
1D
1的棱长为a，P是面对角线AD
1上的动点，点P到BD的距离记为d，求d的最小值，并指出d取最小值时点P的位置．
查看答案和解析>>
科目：gzsx
来源：不详
题型：填空题
设等边△ABC的边长为a，P是△ABC内任意一点，且P到三边AB、BC、CA的距离分别为d
1、d
2、d
3，则有d
1+d
2+d
3为定值
a；由以上平面图形的特性类比到空间图形：设正四面体ABCD的棱长为a，P是正四面体ABCD内任意一点，且P到平面ABC、平面ABD、平面ACD、平面BCD的距离分别为h
1、h
2、h
3、h
4，则有h
1+h
2+h
3+h
4为定值______．
查看答案和解析>>
科目：gzsx
来源：内蒙古包头三十三中2011－2012学年高二下学期期末考试数学文科试题
题型：013
设等边△ABC的边长为a，P是△ABC内的任意一点，且P到三边AB、BC、CA的距离分别为d1、d2、d3，则有d1＋d2＋d3为定值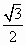
a；由以上平面图形的特性类比空间图形：设正四面体ABCD的棱长为a，P是正四面体ABCD内的任意一点，且P到四个面ABC、ABD、ACD、BCD的距离分别为d1、d2、d3、d4，则有d1＋d2＋d3＋d4为定值
[ ]
A．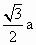
B．
C．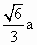
D．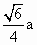
查看答案和解析>>
科目：gzsx
来源：2008年江苏省南通市通州区兴仁中学高二期末数学模拟试卷（解析版）
题型：填空题
设等边△ABC的边长为a，P是△ABC内的任意一点，且P到三边AB，BC，CA的距离分别为d
1，d
2，d
3，则有d
1+d
2+d
3为定值
；由以上平面图形的特性类比空间图形：设正四面体ABCD的棱长为a，P是正四面体ABCD内的任意一点，且P到四个面ABC、ABD、ACD、BCD的距离分别为d
1，d
2，d
3，d
4，则有d
1+d
2+d
3+d
4为定值
．
查看答案和解析>>
科目：gzsx
来源：2011-2012学年江苏省高三数学填空题专练7（解析版）
题型：解答题
设等边△ABC的边长为a，P是△ABC内的任意一点，且P到三边AB，BC，CA的距离分别为d
1，d
2，d
3，则有d
1+d
2+d
3为定值
；由以上平面图形的特性类比空间图形：设正四面体ABCD的棱长为a，P是正四面体ABCD内的任意一点，且P到四个面ABC、ABD、ACD、BCD的距离分别为d
1，d
2，d
3，d
4，则有d
1+d
2+d
3+d
4为定值
．
查看答案和解析>>
科目：gzsx
来源：
题型：
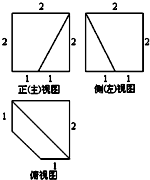
已知一个棱长为2的正方体，被一个平面截后所得几何体的三视图如图所示，则该几何体的体积是（ ）
查看答案和解析>>
棱长为2，点
是正方形
的中心，点
、
分别是棱
的中点．设点
分别是点
内的正投影．
在平面
平面
；