在四边形ABCD中，AB⊥BC，AB=5 BC=12 DA=10答案解析

科目：czsx 来源： 题型：

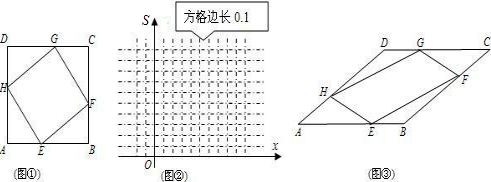
已知：在四边形ABCD中，AB=1，E、F、G、H分别时AB、BC、CD、DA上的点，且AE=BF=CG=DH．设四边形EFGH的面积为S，AE=x（0≤x≤1）．
（1）如图①，当四边形ABCD为正方形时，
①求S关于x的函数解析式，并求S的最小值S₀；
②在图②中画出①中函数的草图，并估计S=0.6时x的近似值（精确到0.01）；
（2）如图③，当四边形ABCD为菱形，且∠A=30°时，四边形EFGH的面积是否存在最小值？若存在，求出最小值；若不存在，请说明理由．

科目：czsx 来源： 题型：

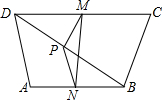
如图所示，在四边形ABCD中，AD=BC，P是对角线BD的中点，M是DC的中点，N是AB的中点．请判断△PMN的形状，并说明理由．

科目：czsx 来源： 题型：

19、在四边形ABCD中，AD=BC，AB=CD．求证：△ABC≌△CDA．

科目：czsx 来源： 题型：

如图，在四边形ABCD中，AB=1，BC=

4

3

，CD=4，AD=

13

3

，∠B=Rt∠，求四边形ABCD的面积．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

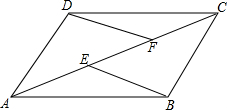
在四边形ABCD中，AB∥CD，AD∥BC，E、F是对角线AC上的两点，AE=CF，证明：
（1）△ABE≌△CDF；    
（2）BE∥DF．

科目：czsx 来源： 题型：

如图1，在正方形ABCD中，E、F分别是BC，CD上的点，且∠EAF=45度．则有结论EF=BE+FD成立；
（1）如图2，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是BC，CD上的点，且∠EAF是∠BAD的一半，那么结论EF=BE+FD是否仍然成立？若成立，请证明；不成立，请说明理由．
（2）若将（1）中的条件改为：在四边形ABCD中，AB=AD，∠B+∠D=180°，延长BC到点E，延长CD到点F，使得∠EAF仍然是∠BAD的一半，则结论EF=BE+FD是否仍然成立？若成立，请证明；不成立，请写出它们的数量关系并证明．

科目：czsx 来源： 题型：

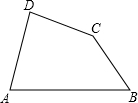
已知：如图，在四边形ABCD中，AD=BC，∠A、∠B均为锐角．
（1）当∠A=∠B时，则CD与AB的位置关系是CD

∥

∥

AB，大小关系是CD

＜

＜

AB；
（2）当∠A＞∠B时，（1）中CD与AB的大小关系是否还成立，证明你的结论．

科目：czsx 来源： 题型：

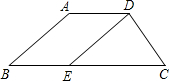
如图，在四边形ABCD中，AD∥BC，BC=8，AD=3，AB=4，CD=3，将AB平移到DE处．
（1）△CDE是直角三角形吗？请说明理由；
（2）求△CDE的边EC上的高；
（3）求四边形ABCD的面积．

科目：czsx 来源： 题型：

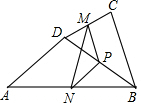
如图，在四边形ABCD中，AD=BC，P是对角线BD的中点，M是边DC的中点，N是边AB的中点．△MPN是什么三角形？为什么？

科目：czsx 来源： 题型：

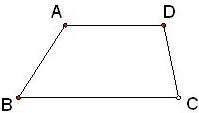
17、如图，在四边形ABCD中，AD∥BC，E为AB的中点．
（1）过点E作直线EF∥BC，交CD于点F；
（2）直线EF与AD是否平行？为什么？
（3）试比较DF与CF的大小．

科目：czsx 来源： 题型：

如图，已知在四边形ABCD中，AB∥CD．直线AB与DE的延长线交于点F，且AB+CD=AF．求证：E是BC的中点．

科目：czsx 来源： 题型：

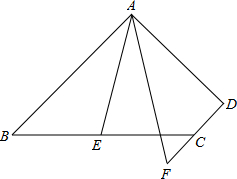
如图，在四边形ABCD中，AB∥CD，点E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F．
（1）若∠D=90°，CD=6，AD=12，AB=18，求AE的长．
（2）求证：AB=AF+CF．

科目：czsx 来源： 题型：

在四边形ABCD中，AD∥BC，∠DCB=90°，AC⊥AB，
（1）求证：△ADC∽△CAB；
（2）若AD=4，BC=9，求sinB．

科目：czsx 来源： 题型：

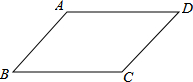
（2013•三明） 如图，在四边形ABCD中，AB∥CD，请你添加一个条件，使得四边形ABCD成为平行四边形，你添加的条件是

答案不唯一，如：AB=CD或AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等

答案不唯一，如：AB=CD或AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等

．

科目：czsx 来源： 题型：

如图，在四边形ABCD中，AD∥BC，E、F为AB上两点，且△DAF≌△CBE．
求证：（1）∠A=90°；
      （2）四边形ABCD是矩形．

科目：czsx 来源： 题型：

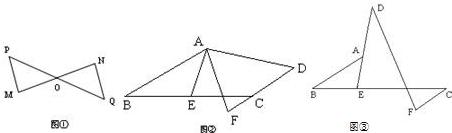
23、如图①，点O为线段MN的中点，PQ与MN相交于点O，且PM∥NQ，可证△PMO≌△QNO．根据上述结论完成下列探究活动：
探究一：如图②，在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F．试探究线段AB与AF、CF之间的数量关系，并证明你的结论；
探究二：如图③，DE、BC相交于点E，BA交DE于点A，且BE：EC=1：2，∠BAE=∠EDF，CF∥AB．若AB=4，CF=2，求DF的长度．

科目：czsx 来源： 题型：

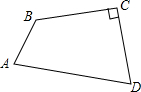
如图，在四边形ABCD中，AB=4-

2

，BC=1，CD=3，∠B=135°，∠C=90°，则∠D等于（　　）

A、60°	B、67.5°
C、75°	D、无法确定

科目：czsx 来源： 题型：

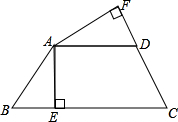
如图，在四边形ABCD中，AB=AD，CA平分∠BCD，AE⊥BC于E，AF⊥CD交CD延长线于F．求证：BE=DF．

科目：czsx 来源： 题型：

如图，在四边形ABCD中，AB=4，BC=3，CD=12，AD=13，∠B=90°，求四边形ABCD的面积．