科目:czsx
来源:北京中考真题
题型:解答题
已知二次函数y=(t+1)x
2+2(t+2)x+

,在x=0和x=2时的函数值相等。
(1)求二次函数解析式;
(2)若一次函数y=kx+6的图像与二次函数的图像都经过点A(-3,m),求m和k的值;
(3)设二次函数的图象与x轴交于点B,C(点C在点B,C的左侧),将二次函数的图象在点B,C间的部分(含点C和点C)向左平移n(n>0)个单位后得到的图象记为G,同时将(2)中得到的直线y=kx+6向上平移n个单位。请结合图象回答:当平移后的直线与图象G有公共点时,n的取值范围。
查看答案和解析>>
科目:czsx
来源:专项题
题型:解答题
已知二次函数
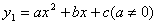
的图象经过三点(1,0),(-3,0),(0,
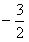
)。
(1)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像;
(2)若反比例函数
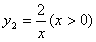
的图像与二次函数
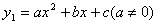
的图像在第一象限内交于点A(x
0,y
0),x
0落在两个相邻的正整数之间。请你观察图像,写出这两个相邻的正整数;
(3)若反比例函数
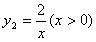
的图像与二次函数
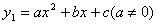
的图像在第一象限内的交点为A,点A的横坐标为x
0满足2<x
0<3,试求实数k的取值范围。
查看答案和解析>>
科目:czsx
来源:2008年江苏省泰州市初中毕业、升学统一考试数学试题
题型:044
已知二次函数y1=ax2+bx+c(a≠0)的图像经过三点(1,0),(-3,0),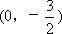 .
.
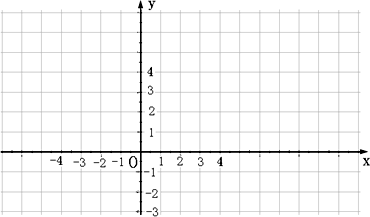
(1)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像;
(2)若反比例函数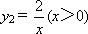 的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内交于点A(x0,y0),x0落在两个相邻的正整数之间,请你观察图像,写出这两个相邻的正整数;
的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内交于点A(x0,y0),x0落在两个相邻的正整数之间,请你观察图像,写出这两个相邻的正整数;
(3)若反比例函数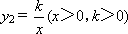 的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内的交点A,点A的横坐标x0满足2<x0<3,试求实数k的取值范围.
的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内的交点A,点A的横坐标x0满足2<x0<3,试求实数k的取值范围.
查看答案和解析>>
科目:czsx
来源:江苏期中题
题型:解答题
已知反比例函数

的图像与二次函数

的图像相交于点(2,2).
(1)求a和k的值;
(2)反比例函数的图像是否经过二次函数图像的顶点,为什么?
查看答案和解析>>
科目:czsx
来源:新课标3维同步训练与评价数学 九年级(下)
题型:044
二次函数y=-3x2+1的图像与二次函数y=-3x2的图像有什么关系?它是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?先想一想,如果需要,作草图看一看,二次函数y=- x2+1与y=-
x2+1与y=-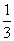 x2呢?
x2呢?
查看答案和解析>>
科目:czsx
来源:新课标3维同步训练与评价数学 九年级(下)
题型:044
二次函数y=3x2的图像与二次函数y=-3x2的图像有什么关系?它是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?先想一想,如果需要,作草图看一看,二次函数y=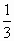 x2与y=-
x2与y=-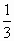 x2呢?
x2呢?
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上,P为线段AB上一动点(除A,B两端点外),过P作x轴的垂线与二次函数的图象交于点Q设线段PQ的长为l,点P的横坐标为x.
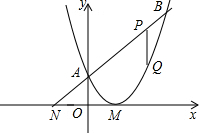
(1)求二次函数的解析式;
(2)求l与x之间的函数关系式,并求出l的取值范围;
(3)线段AB上是否存在一点P,使四边形PQMA为梯形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上,P为线段AB上一动点(除A,B两端点外),过P作x轴的垂线与二次函数的图象交

于点Q,设线段PQ的长为l,点P的横坐标为x.
(1)求出l与x之间的函数关系式,并求出l的取值范围;
(2)在线段AB上是否存在一点P,使四边形PQMA为梯形?若存在,求出点P的坐标及梯形PQMA的面积;若不存在,请说明理由;
(3)当2<x<6时,延长PQ、AM交于F,连接NF、PM,求证:NF⊥PM.
查看答案和解析>>
科目:czsx
来源:
题型:
已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示)
(1)求该二次函数的解析式;
(2)P为线段AB上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为l,点P的横坐标为x,求出l与x之间的函数关系式,并求出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在一点P,使四边形PQMA为梯形?若存在
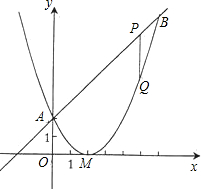
,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012年北师大版初中数学九年级下2.8二次函数与一元二次方程练习卷(解析版)
题型:解答题
一元二次方程x2+7x+9=1的根与二次函数y=x2+7x+9的图像有什么关系?
试把方程的根在图像上表示出来.
查看答案和解析>>
科目:czsx
来源:第26章《二次函数》中考题集(47):26.3 实际问题与二次函数(解析版)
题型:解答题
已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示)
(1)求该二次函数的解析式;
(2)P为线段AB上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为l,点P的横坐标为x,求出l与x之间的函数关系式,并求出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在一点P,使四边形PQMA为梯形?若存在,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2005年福建省龙岩市中考数学试卷(大纲卷)(解析版)
题型:解答题
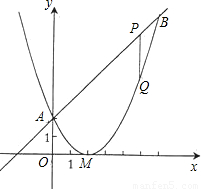
(2005•龙岩)已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示)
(1)求该二次函数的解析式;
(2)P为线段AB上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为l,点P的横坐标为x,求出l与x之间的函数关系式,并求出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在一点P,使四边形PQMA为梯形?若存在,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(49):2.3 二次函数的应用(解析版)
题型:解答题
已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示)
(1)求该二次函数的解析式;
(2)P为线段AB上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为l,点P的横坐标为x,求出l与x之间的函数关系式,并求出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在一点P,使四边形PQMA为梯形?若存在,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
已知一次函数 的图像和二次函数
的图像和二次函数 的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5.
的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5.

(1)求这个二次函数的解析式;
(2)将此二次函数图像的顶点记作点P,求△ABP的面积;
(3)已知点C、D在射线AB上,且D点的横坐标比C点的横坐标大2,点E、F在这个二次函数图像上,且CE、DF与y轴平行,当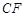 ∥
∥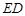 时,求C点坐标.
时,求C点坐标.
【解析】二次函数的综合运用
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上,P为线段AB上一动点(除A,B两端点外),过P作x轴的垂线与二次函数的图象交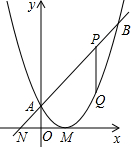 于点Q,设线段PQ的长为l,点P的横坐标为x.
于点Q,设线段PQ的长为l,点P的横坐标为x.
(1)求出l与x之间的函数关系式,并求出l的取值范围;
(2)在线段AB上是否存在一点P,使四边形PQMA为梯形?若存在,求出点P的坐标及梯形PQMA的面积;若不存在,请说明理由;
(3)当2<x<6时,延长PQ、AM交于F,连接NF、PM,求证:NF⊥PM.
查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(46):23.5 二次函数的应用(解析版)
题型:解答题
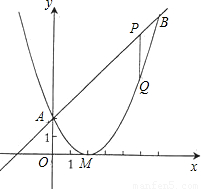
已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示)
(1)求该二次函数的解析式;
(2)P为线段AB上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为l,点P的横坐标为x,求出l与x之间的函数关系式,并求出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在一点P,使四边形PQMA为梯形?若存在,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012年广东省广州市花都区中考数学一模试卷(解析版)
题型:解答题
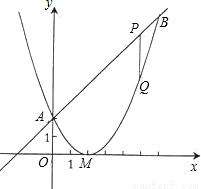
已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示)
(1)求该二次函数的解析式;
(2)P为线段AB上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为l,点P的横坐标为x,求出l与x之间的函数关系式,并求出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在一点P,使四边形PQMA为梯形?若存在,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第27章《二次函数》中考题集(49):27.3 实践与探索(解析版)
题型:解答题
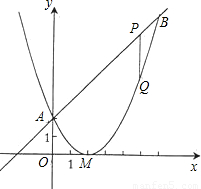
已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示)
(1)求该二次函数的解析式;
(2)P为线段AB上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为l,点P的横坐标为x,求出l与x之间的函数关系式,并求出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在一点P,使四边形PQMA为梯形?若存在,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2011-2012学年上海市黄浦区九年级中考二模数学卷(解析版)
题型:解答题
已知一次函数 的图像和二次函数
的图像和二次函数 的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5.
的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5.
(1)求这个二次函数的解析式;
(2)将此二次函数图像的顶点记作点P,求△ABP的面积;
(3)已知点C、D在射线AB上,且D点的横坐标比C点的横坐标大2,点E、F在这个二次函数图像上,且CE、DF与y轴平行,当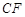 ∥
∥ 时,求C点坐标.
时,求C点坐标.
【解析】二次函数的综合运用
查看答案和解析>>

 ,在x=0和x=2时的函数值相等。
,在x=0和x=2时的函数值相等。
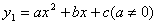 的图象经过三点(1,0),(-3,0),(0,
的图象经过三点(1,0),(-3,0),(0,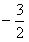 )。
)。 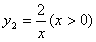 的图像与二次函数
的图像与二次函数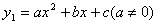 的图像在第一象限内交于点A(x0,y0),x0落在两个相邻的正整数之间。请你观察图像,写出这两个相邻的正整数;
的图像在第一象限内交于点A(x0,y0),x0落在两个相邻的正整数之间。请你观察图像,写出这两个相邻的正整数;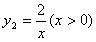 的图像与二次函数
的图像与二次函数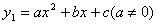 的图像在第一象限内的交点为A,点A的横坐标为x0满足2<x0<3,试求实数k的取值范围。
的图像在第一象限内的交点为A,点A的横坐标为x0满足2<x0<3,试求实数k的取值范围。 ![]() 的图象经过三点(1,0),(-3,0),(0,
的图象经过三点(1,0),(-3,0),(0,![]() )。
)。![]() 图像与二次函数
图像与二次函数![]() 的图像在第一象限内交于点A(x0,y0), x0落在两个相邻的正整数之间。请你观察图像,写出这两个相邻的正整数;
的图像在第一象限内交于点A(x0,y0), x0落在两个相邻的正整数之间。请你观察图像,写出这两个相邻的正整数; ![]() 的图像与二次函数
的图像与二次函数![]() 的图像在第一象限内的交点为A,点A的横坐标为
的图像在第一象限内的交点为A,点A的横坐标为![]() 满足2<
满足2<![]() <3,试求实数k的取值范围。
<3,试求实数k的取值范围。
![]() .
.
![]() 的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内交于点A(x0,y0),x0落在两个相邻的正整数之间,请你观察图像,写出这两个相邻的正整数;
的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内交于点A(x0,y0),x0落在两个相邻的正整数之间,请你观察图像,写出这两个相邻的正整数;![]() 的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内的交点A,点A的横坐标x0满足2<x0<3,试求实数k的取值范围.
的图像与二次函数y1=ax2+bx+c(a≠0)的图像在第一象限内的交点A,点A的横坐标x0满足2<x0<3,试求实数k的取值范围.
 的图像与二次函数
的图像与二次函数 的图像相交于点(2,2).
的图像相交于点(2,2). ![]() x2+1与y=-
x2+1与y=-![]() x2呢?
x2呢?![]() x2与y=-
x2与y=-![]() x2呢?
x2呢?
 于点Q,设线段PQ的长为l,点P的横坐标为x.
于点Q,设线段PQ的长为l,点P的横坐标为x. ,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.
,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由. 


![]() 的图像和二次函数
的图像和二次函数![]() 的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5.
的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5. 
![]() ∥
∥![]() 时,求C点坐标.
时,求C点坐标. 于点Q,设线段PQ的长为l,点P的横坐标为x.
于点Q,设线段PQ的长为l,点P的横坐标为x.


 的图像和二次函数
的图像和二次函数 的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5.
的图像都经过A、B两点,且点A在y轴上,B点的纵坐标为5. 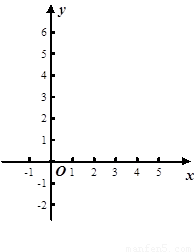
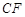 ∥
∥ 时,求C点坐标.
时,求C点坐标.