
科目:czsx 来源: 题型:
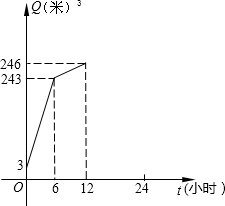 水管.如图表示水塔中的储水量Q(米3)与时间t(小时)之间的函数图象.
水管.如图表示水塔中的储水量Q(米3)与时间t(小时)之间的函数图象.科目:czsx 来源: 题型:
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -6 | -6 | 0 | 2 | 0 | -6 |
科目:czsx 来源: 题型:
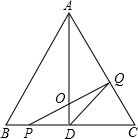 如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D.点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D.点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).科目:czsx 来源: 题型:
| 3 |
| 3 |
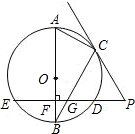 ?试写出你的猜想,并说明理由.
?试写出你的猜想,并说明理由. 科目:czsx 来源: 题型:
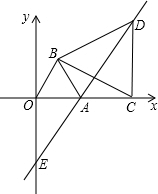 OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
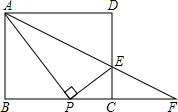 出它的定义域;
出它的定义域;| 1 | 2 |
科目:czsx 来源: 题型:
| A、12 | B、11 | C、10 | D、9 |
科目:czsx 来源: 题型:
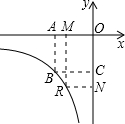 如图,正方形OABC的面积是4,点B在反比例函数y=
如图,正方形OABC的面积是4,点B在反比例函数y=| k | x |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| 1 |
| x |
| 1 |
| x |
科目:czsx 来源: 题型:
