
科目:gzsx 来源: 题型:
科目:gzsx 来源:专项题 题型:解答题
科目:gzsx 来源:2009年广东省广州市高考数学二模试卷(文科)(解析版) 题型:解答题
科目:gzsx 来源:2009年广东省广州市高考数学二模试卷(理科)(解析版) 题型:解答题
科目:gzsx 来源: 题型:
科目:gzsx 来源:2010年上海市上海中学高三数学综合练习试卷(8)(解析版) 题型:解答题
 ,
,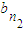 ,…,
,…, ,…成等比数列,求数列{nt}的通项公式(t是正整数);
,…成等比数列,求数列{nt}的通项公式(t是正整数);科目:gzsx 来源: 题型:
科目:gzsx 来源:不详 题型:解答题
科目:gzsx 来源:2012-2013学年上海外国语大学附中高三(上)第一次周练数学试卷(解析版) 题型:解答题
 ;
;科目:gzsx 来源: 题型:
|
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
g(
| ||
| dn+1 |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| 1 | x |
科目:gzsx 来源: 题型:
| 1 |
| an |
| 1 |
| an |
| 1 |
| an+1 |
科目:gzsx 来源: 题型:
| 2x-1 |
科目:gzsx 来源: 题型:
| 5x-a | x+2 |