an+1=根号(3+an)/2,试求a1的值使的数列an是一个常数数列答案解析
科目:gzsx
来源:
题型:
(2012•闵行区三模)已知数列{a
n}中,a
1>0,
an+1=(n∈N
*).
(1)试求a
1的值,使数列{a
n}是一个常数列;
(2)试求a
1的取值范围,使得数列{a
n}是单调增数列;
(3)若{a
n}不为常数列,设b
n=|a
n+1-a
n|(n∈N
*),S
n为数列{b
n}的前n项和,请你写出a
1的一个值,使得
Sn<恒成立,并说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数y=f(x)(x∈R)对任意实数x,y,有
f(x)+f(y)=2f()•f()恒成立,且f(0)≠0
(1)求f(0)的值;
(2)试判断函数y=f(x)(x∈R)的奇偶性;
(3)若函数y=f(x)(x∈R)在[0,+∞)上单调递增,f(x-1)-2a+3≥0恒成立,试求a的取值范围.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年河南省中原名校高一(上)期中数学试卷B(解析版)
题型:解答题
已知函数y=f(x)(x∈R)对任意实数x,y,有

恒成立,且f(0)≠0
(1)求f(0)的值;
(2)试判断函数y=f(x)(x∈R)的奇偶性;
(3)若函数y=f(x)(x∈R)在[0,+∞)上单调递增,f(x-1)-2a+3≥0恒成立,试求a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知函数y=f(x)(x∈R)对任意实数x,y,有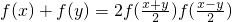 恒成立,且f(0)≠0
恒成立,且f(0)≠0
(1)求f(0)的值;
(2)试判断函数y=f(x)(x∈R)的奇偶性;
(3)若函数y=f(x)(x∈R)在[0,+∞)上单调递增,f(x-1)-2a+3≥0恒成立,试求a的取值范围.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年河南省中原名校高一(上)期中数学试卷B(解析版)
题型:解答题
已知函数y=f(x)(x∈R)对任意实数x,y,有

恒成立,且f(0)≠0
(1)求f(0)的值;
(2)试判断函数y=f(x)(x∈R)的奇偶性;
(3)若函数y=f(x)(x∈R)在[0,+∞)上单调递增,f(x-1)-2a+3≥0恒成立,试求a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
数列{a
n}中,a
1=1,
an+1=2an-n2+3n,(n∈N
*).
(1)求a
2,a
3的值;
(2)试求λ、μ的值,使得数列
{an+λn2+μn}为等比数列;
(3)设数列{b
n}满足:
bn=,S
n为数列{b
n}的前n项和.证明:n≥2时,
<Sn<.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2008•普陀区二模)已知无穷数列{a
n}中,a
1,a
2,…,a
m是以10为首项,以-2为公差的等差数列;a
m+1,a
m+2,…,a
2m是以
为首项,以
为公比的等比数列(m≥3,m∈N
*);并且对一切正整数n,都有a
n+2m=a
n成立.
(1)当m=3时,请依次写出数列{a
n}的前12项;
(2)若a
23=-2,试求m的值;
(3)设数列{a
n}的前n项和为S
n,问是否存在m的值,使得S
128m+3≥2008成立?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知数列{a
n}的前n项和为S
n,满足关系式(2+t)S
n+1-tS
n=2t+4(t≠-2,t≠0,n=1,2,3,…).
(Ⅰ)当a
1为何值时,数列{a
n}是等比数列;
(Ⅱ)在(Ⅰ)的条件下,设数列{a
n}的公比为f(t),作数列{b
n}使b
1=1,b
n=f(b
n-1)(n=2,3,4,…),求b
n;
(Ⅲ)在(Ⅱ)条件下,如果对一切n∈N
+,不等式
bn+bn+1<恒成立,求实数c的取值范围.
查看答案和解析>>
科目:gzsx
来源:宜春市2007届高三年级第一次模拟考试
题型:044
己知数列{an}满足 ,其中n∈N*,首项为a1
,其中n∈N*,首项为a1
(1)若数列是一个无穷的常数数列,试求a1的值.
(2)若a1=2,求满足不等式 的自然数n的集合
的自然数n的集合
(3)若存在a1=m,使数列{an}满足,对任意的正整数n,均有 .求m的取值范围.
.求m的取值范围.
查看答案和解析>>
科目:gzsx
来源:2008年上海市普陀区高考数学二模试卷(解析版)
题型:解答题
已知无穷数列{a
n}中,a
1,a
2,…,a
m是以10为首项,以-2为公差的等差数列;a
m+1,a
m+2,…,a
2m是以

为首项,以

为公比的等比数列(m≥3,m∈N
*);并且对一切正整数n,都有a
n+2m=a
n成立.
(1)当m=3时,请依次写出数列{a
n}的前12项;
(2)若a
23=-2,试求m的值;
(3)设数列{a
n}的前n项和为S
n,问是否存在m的值,使得S
128m+3≥2008成立?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
数列{a
n}中,a
1=1,
an+1=2an-n2+3n,(n∈N
*).
(1)求a
2,a
3的值;
(2)试求λ、μ的值,使得数列
{an+λn2+μn}为等比数列;
(3)设数列{b
n}满足:
bn=,S
n为数列{b
n}的前n项和.证明:n≥2时,
<Sn<.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年广东省深圳市南山区高三(上)期末数学试卷(理科)(解析版)
题型:解答题
数列{a
n}中,a
1=1,

,(n∈N
*).
(1)求a
2,a
3的值;
(2)试求λ、μ的值,使得数列

为等比数列;
(3)设数列{b
n}满足:

,S
n为数列{b
n}的前n项和.证明:n≥2时,

.
查看答案和解析>>
科目:gzsx
来源:2008年高考冲刺解答题突破、数学
题型:044
已知数列{an}满足an+1=an+2,Sn是其前n项和,且S3=9,二次函数f(x)=snx2+anx-2的图象与x轴有两个交点(x1,0)和(x2,0),且-3<x1<-1<x2<2,试求n的值.
查看答案和解析>>
科目:gzsx
来源:2010年广东省珠海五中高考数学模拟试卷(文科)(解析版)
题型:解答题
已知数列{a
n}的前n项和为S
n,满足关系式(2+t)S
n+1-tS
n=2t+4(t≠-2,t≠0,n=1,2,3,…).
(Ⅰ)当a
1为何值时,数列{a
n}是等比数列;
(Ⅱ)在(Ⅰ)的条件下,设数列{a
n}的公比为f(t),作数列{b
n}使b
1=1,b
n=f(b
n-1)(n=2,3,4,…),求b
n;
(Ⅲ)在(Ⅱ)条件下,如果对一切n∈N
+,不等式

恒成立,求实数c的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知数列{an}的前n项和为Sn,满足关系式(2+t)Sn+1-tSn=2t+4(t≠-2,t≠0,n=1,2,3,…).
(Ⅰ)当a1为何值时,数列{an}是等比数列;
(Ⅱ)在(Ⅰ)的条件下,设数列{an}的公比为f(t),作数列{bn}使b1=1,bn=f(bn-1)(n=2,3,4,…),求bn;
(Ⅲ)在(Ⅱ)条件下,如果对一切n∈N+,不等式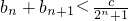 恒成立,求实数c的取值范围.
恒成立,求实数c的取值范围.
查看答案和解析>>
科目:gzsx
来源:2008-2009学年上海市普陀区曹杨二中高三(上)入学摸底数学试卷(解析版)
题型:解答题
已知无穷数列{a
n}中,a
1,a
2,…,a
m是以10为首项,以-2为公差的等差数列;a
m+1,a
m+2,…,a
2m是以

为首项,以

为公比的等比数列(m≥3,m∈N
*);并且对一切正整数n,都有a
n+2m=a
n成立.
(1)当m=3时,请依次写出数列{a
n}的前12项;
(2)若a
23=-2,试求m的值;
(3)设数列{a
n}的前n项和为S
n,问是否存在m的值,使得S
128m+3≥2008成立?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
设{a
n}为递增等差数列,S
n为其前n项和,满足a
1a
3-a
5=S
10,S
11=33.
(1)求数列{a
n}的通项公式a
n及前n项和S
n;
(2)试求所有的正整数m,使
为正整数.
查看答案和解析>>
科目:gzsx
来源:
题型:
设a
n是公差不为零的等差数列,S
n为其前n项和,满足a
22+a
32=a
42+a
52,S
7=7
(1)求数列a
n的通项公式及前n项和S
n;
(2)试求所有的正整数m,使得
为数列a
n中的项.
查看答案和解析>>
科目:gzsx
来源:
题型:
(1)已知{a
n}是公差为-2的等差数列,a
7是a
3与a
9的等比中项,求该数列前10项和S
10;
(2)若数列{b
n}满足b
1=
,b
n+1=
,试求b
2013的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
设数列{an}是公差不为0的等差数列,Sn为前n项和,满足a3,2a5,a12成等差数列,S10=60.
(1)求数列{an}的通项公式及前n项和Sn;
(2)试求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>

 恒成立,且f(0)≠0
恒成立,且f(0)≠0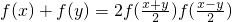 恒成立,且f(0)≠0
恒成立,且f(0)≠0 恒成立,且f(0)≠0
恒成立,且f(0)≠0![]() ,其中n∈N*,首项为a1
,其中n∈N*,首项为a1![]() 的自然数n的集合
的自然数n的集合![]() .求m的取值范围.
.求m的取值范围. 为首项,以
为首项,以 为公比的等比数列(m≥3,m∈N*);并且对一切正整数n,都有an+2m=an成立.
为公比的等比数列(m≥3,m∈N*);并且对一切正整数n,都有an+2m=an成立. ,(n∈N*).
,(n∈N*). 为等比数列;
为等比数列; ,Sn为数列{bn}的前n项和.证明:n≥2时,
,Sn为数列{bn}的前n项和.证明:n≥2时, .
. 恒成立,求实数c的取值范围.
恒成立,求实数c的取值范围.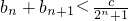 恒成立,求实数c的取值范围.
恒成立,求实数c的取值范围. 为首项,以
为首项,以 为公比的等比数列(m≥3,m∈N*);并且对一切正整数n,都有an+2m=an成立.
为公比的等比数列(m≥3,m∈N*);并且对一切正整数n,都有an+2m=an成立.